Up: Table of Contents
Prev: Bifurcation

Questions on One-Dimensional Dynamical Systems

Questions on Part 2

    Eventual behavior

  1. What are the fixed points of f(x) = x2?

    What is the relation between the fixed points of the square function and the intersection points of the graph of the square function with the special lines y = x and y = -x?

  2. Consider the square function on your calculator. Pick a point "near" (distance less than 0.1 is near enough) a fixed point. Keep iterating (pushing the squaring button) until you see a pattern for the long term behavior. Try again with other numbers near each of the fixed points. Write down what happens for each choice. Does it matter if the number you pick is less than or greater than the fixed point?

  3. Which of the fixed points for the square function are attracting? Which are repelling?

    Questions on Part 3

    Iterates versus time

  4. Use the Java Applet Iterates versus time for the Logistic map to see how the plot changes as lambda varies. Describe what you see.

    Note that always the iterates of x0 = 0.5 are taken. Can you find values for x0 (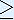>= 0) for which the orbit behaves different from the orbit of x0 = 0.5?

    Graphical iteration

  5. Use the Java Applet Iteration of the Logistic Map to see how the dynamics close to the (positive) fixed point depends on the parameter lambda. When you start the applet, this fixed point is attracting. Is it attracting for all x0? Is it attracting for all lambda? If not, what happens right after it stopped being attracting?

  6. Use the Java Applet The Period Doubling Route to Chaos for this question. If you know how to work with Devaney's Chaos Lab #2, or the Mathematica package, you can use these as well.

    Fix the starting point x0 = 0.1. For several choices of lambda between 0 and 3.5, investigate the eventual behavior of x0 = 0.1. In Devaney's Chaos Lab #2 you can push the Transient button to see what the eventual behavior is; in the other cases, the eventual behavior is shown in red.

    Draw a diagram with lambda on the horizontal axis and x on the vertical axis. For each lambda value that you checked, place a dot at the x values that are part of the eventual behavior of x0 = 0.1. If you checked the eventual behavior for enough lambda values, you should be able to sketch the curves connecting the dots, showing the continuous dependence on lambda. Do not go beyond lambda = 3.5.

    Questions on Part 4

    Periodic points

  7. Algebraically verify that +1 and -1 are fixed points of the function f(x) = 1/x.

  8. Algebraically verify that 0 is a fixed point of the "+/-" function.

  9. Algebraically find the fixed points of the square root function.

  10. What is the period of a point under application of the "+/-" button?

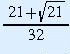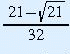  11. Check that for f(x) = 3.2 x (1 - x), the points x = 0 and x = 11/16 are fixed points. Check that x = (21 + sqrt(21))/32 and x = (21 - sqrt(21))/32 are period-2 points.

  12. Draw the graphs of the first and second iterate of the Logistic map for lambda = 3.2. Check graphically the number of points of least period 2. Does this agree with what you found in the previous question?

  13. Graphically determine the number of period-2 points for functions in the Logistic family at lambda = 2, 3.1, and 3.5. Remember to exclude fixed points when you count intersections. Are they attracting?

    Eventual behavior

  14. Using the techniques from the part on Eventual behavior, draw a qualitative diagram for the eventual behavior of all points under the Logistic map for lambda = 2. Your diagram does not need to have exact values of fixed and periodic points. The idea is to compare pictures qualitatively.

  15. Using the techniques from the part on Eventual behavior, draw a qualitative diagram for lambda = 3.1. As you investigate, magnify the region near the fixed point other than 0. Compared to the behavior for lambda = 2, what has happened?

  16. Using the techniques from the part on Eventual behavior, draw a qualitative diagram for lambda = 3.5. What is the period of the attracting orbit here? Indicate in which order the points in the orbit occur.

    Hartman and Grobman

  17. Compare the figure for lambda = 2.5 with the figure for lambda = 1.5. What is the difference in behavior of the graphical iterations? Why do you think this difference is there? (Hint: look at the slope of the graph at the attracting fixed point.)

  18. Recall that in order to find period-2 points, you graphed the second iterate of the map. Can you find a relationship between the slope of the graph of the second iterate of the function and whether the period-2 points are attracting, repelling, or neutral?

  19. Describe geometrically how your relationship (between the slope of the graph of the second iterate of the function and whether the period-2 points are attracting, repelling, or neutral) might generalize to period-n points.

    Questions on Part 5

    Qualitative change of dynamics

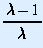  20. Recall that p is a fixed point of f if f(p) = p. Verify that the Logistic family f(x) = lambdax (1 - x) has fixed points x = 0 and x = (lambda-1) over lambda.

    The slope of the graph of the Logistic map at a fixed point p can be computed as follows: Determine the derivative of f with respect to x. Then replace any x in the derivative with p. This expression is exactly the requested slope.

    Compute the slope of the graph of the Logistic map at the fixed point 0 in terms of lambda. What is the slope for the other fixed point?

  21. For what values of lambda are the fixed points of the Logistic family attracting? Repelling? Neutral? Test your values using the computer.

    Bifurcation points

  22. Approximately at what lambda value between 1.5 and 3.1 does a bifurcation occur?

  23. At exactly what lambda value between 1.5 and 3.1 does a bifurcation occur? Explain why you know this value is exact.

    Orbit diagram

  24. Consider the orbit diagram for the Logistic map. At lambda = 1 the curve suddenly turns away from the horizontal axis. What has happened?

  25. Somewhere between 2 and 3.1, the orbit diagram curve splits into two branches. Why are there two branches now? What do they correspond to? (Hint: What was the eventual behavior of points in this region?)

  26. Investigate further bifurcations as lambda increases. Describe the sequence of bifurcations. In other words, how does the period of the attracting set change at each bifurcation?

    General Questions on One-Dimensional Dynamical Systems

  27. In Devaney's Chaos Lab #2, pick "Quadratic" under the Function menu. In Mathematica, type << Quadratic.m after you loaded the package Chaos.m. Your dynamical system is now

    f(x) = x2 + lambda.


    In Devaney's Chaos Lab, lambda = c.

    Investigate the behavior of the iterates for parameters in a small interval around lambda = -0.75. Discuss the bifurcation that occurs in the Quadratic family for lambda = -0.75.

  28. Pick "Sine" under the Function menu in Devaney's Chaos Lab #2. In Mathematica, load the package Chaos.m, then type << Sine.m. Your dynamical system is now

    f(x) = lambda Sin(x).


    In Devaney's Chaos Lab, lambda = A.

    Investigate the behavior of the iterates for parameters in a small interval around lambda = 1. Discuss the bifurcation that occurs in the Sine family for lambda = 1.

  29. Use either Devaney's Chaos Lab #3 of Mathematica. Compare the orbit diagrams for the Logistic family f(x) = lambdax (1 - x) and for the Quadratic family f(x) = x2 + lambda. Do you see any similarities? Discuss them and point out the differences.

    What is the range of lambda values in the diagram for the Logistic family? What is the range of lambda values in the diagram for the Quadratic family?

    For lambda = 4, the graph of the Logistic map is special. The interval [0,1/2] is mapped entirely onto [0,1] and also the interval [1/2,1] is mapped entirely onto [0,1]. The Logistic map covers the interval [0,1] twice. Notice that this is not true for smaller (positive) values of lambda.

    Find the value for lambda such that the graph of f(x) = x2 + lambda covers the interval [-2,2] exactly twice, as described above for the Logistic map.

Up: Table of Contents
Prev: Bifurcation
[HOME] The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 9 1998 --- Last modified: Wed May 13 15:16:40 1998