Next:
Questions on One-Dimensional Dynamical Systems
Up: Table of Contents
Prev:
Linear and Nonlinear Behavior
One-Dimensional Dynamical Systems
Part 5: Bifurcation
The dynamics of a function is a qualitative description of the
eventual behavior of all points on the line. This includes information
such as the number and relative placement of fixed and periodic points
and whether they are attracting, repelling, or neutral. If the
function depends on a parameter, the dynamics of this function
depends on the parameter as well.
Parameter dependent dynamics
As the parameter
 of the
Logistic map increases, a series of period-doubling bifurcations
occur. The Logistic map becomes chaotic for even larger
of the
Logistic map increases, a series of period-doubling bifurcations
occur. The Logistic map becomes chaotic for even larger
 (certainly for
(certainly for

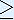 4).
We say that the Logistic map becomes chaotic as it undergoes a series
of period-doubling bifurcations. In fact, this is a typical route to
chaos, which is not at all restricted to the Logistic map alone. We
never gave a definition of chaotic behavior, and we are not
going to, but you can think of a dynamical system being chaotic if it
has periodic points of any period, which are all repelling.
4).
We say that the Logistic map becomes chaotic as it undergoes a series
of period-doubling bifurcations. In fact, this is a typical route to
chaos, which is not at all restricted to the Logistic map alone. We
never gave a definition of chaotic behavior, and we are not
going to, but you can think of a dynamical system being chaotic if it
has periodic points of any period, which are all repelling.
Before a map can possibly have infinitely many periodic points with
distinct periods, it must have periodic points with all periods of the
form 2n. If for a particular parameter value a
periodic point of period 5 appears, you can imagine how periodic
points of periods 10, 20, 40, etc. are born as the parameter is
increased. In fact, there is a very strict, and universal, ordering of
the periods described in a famous paper by Li and Yorke called
Period 3 implies Chaos. You can read more about this in the
Geometry Forum article
Sharkovskii's Theorem.
Next:
Questions on One-Dimensional Dynamical Systems
Up: Table of Contents
Prev:
Linear and Nonlinear Behavior
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Written by Hinke Osinga
Comments to:
webmaster@geom.umn.edu
Created: Apr 6 1998 ---
Last modified: Thu Apr 9 14:41:02 1998
 of the
Logistic map increases, a series of period-doubling bifurcations
occur. The Logistic map becomes chaotic for even larger
of the
Logistic map increases, a series of period-doubling bifurcations
occur. The Logistic map becomes chaotic for even larger
 (certainly for
(certainly for

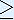 4).
We say that the Logistic map becomes chaotic as it undergoes a series
of period-doubling bifurcations. In fact, this is a typical route to
chaos, which is not at all restricted to the Logistic map alone. We
never gave a definition of chaotic behavior, and we are not
going to, but you can think of a dynamical system being chaotic if it
has periodic points of any period, which are all repelling.
4).
We say that the Logistic map becomes chaotic as it undergoes a series
of period-doubling bifurcations. In fact, this is a typical route to
chaos, which is not at all restricted to the Logistic map alone. We
never gave a definition of chaotic behavior, and we are not
going to, but you can think of a dynamical system being chaotic if it
has periodic points of any period, which are all repelling.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page