Up: Bifurcation
One-Dimensional Dynamical Systems
Part 5: Bifurcation
Qualitative change of dynamics
The theorem of Hartman
and Grobman gives us the relationship between the slope of the graph
at a fixed point and whether this fixed point is attracting, repelling,
or neutral. For the Logistic map, we have already seen that the fixed
point other than 0 is attracting for
 = 1.5, because
the slope is between -1 and 1. However, it is repelling for
= 1.5, because
the slope is between -1 and 1. However, it is repelling for
 = 3.1, since
the graph of the derivative map no longer has a slope between -1 and
1. Hence, as we increase
= 3.1, since
the graph of the derivative map no longer has a slope between -1 and
1. Hence, as we increase
 , the fixed
point changes from being attracting to being repelling. This scenario
is called a bifurcation.
, the fixed
point changes from being attracting to being repelling. This scenario
is called a bifurcation.
- Recall that
p is a fixed point of f if f(p) =
p. Verify that the Logistic family
f(x) =
 x
(1 - x) has fixed points x = 0 and x =
x
(1 - x) has fixed points x = 0 and x =
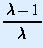 .
.
Compute the slope of the graph of the Logistic map at the fixed point
0 in terms of
 . What is the
slope for the other fixed point?
. What is the
slope for the other fixed point?
- For what values of
 are the fixed
points of the Logistic family attracting? Repelling? Neutral? Test
your values using the computer.
are the fixed
points of the Logistic family attracting? Repelling? Neutral? Test
your values using the computer.
Up: Bifurcation
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Written by Hinke Osinga
Comments to:
webmaster@geom.umn.edu
Created: Apr 6 1998 ---
Last modified: Thu Apr 9 14:18:16 1998
 = 1.5, because
the slope is between -1 and 1. However, it is repelling for
= 1.5, because
the slope is between -1 and 1. However, it is repelling for
 = 3.1, since
the graph of the derivative map no longer has a slope between -1 and
1. Hence, as we increase
= 3.1, since
the graph of the derivative map no longer has a slope between -1 and
1. Hence, as we increase
 , the fixed
point changes from being attracting to being repelling. This scenario
is called a bifurcation.
, the fixed
point changes from being attracting to being repelling. This scenario
is called a bifurcation.
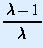 .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page