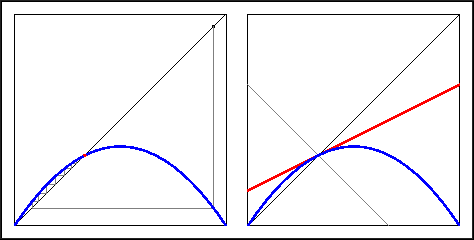
The fixed point other than 0 is attracting for
 = 1.5.
= 1.5.
One-Dimensional Dynamical Systems
Part 4: Linear and Nonlinear Behavior
Hartman and Grobman
Locally near a point x, a differential function can be
approximated by its derivative at x. That is, the graph of
the function locally near x is almost equal to a straight
line with a slope equal to the derivative at x. Hence, the
derivative Df(x) at a specific point x can
be interpreted as a (linear) map, that has this straight line as its
graph. This map is called the derivative map. However, if the
functions are almost the same near x, what about the behavior
of the two dynamical systems?
Note that the theorem is only true on a small neighborhood of the fixed point p. In particular if other fixed points or periodic points are close to p, this neighborhood is very small! You can now find a relationship between the slope of the graph at the fixed point and whether the fixed point is attracting, repelling, or neutral.

The fixed point other than 0 is attracting for
 = 1.5.
= 1.5.
Recall your investigations in the Warm Up Questions. In the figure above (right) the graph of the derivative map at the fixed point is drawn in read. Also drawn are the two special lines with slope 1 and -1. The figure clearly shows that the derivative at the fixed point lies in between -1 and 1, so that the fixed point is attracting.
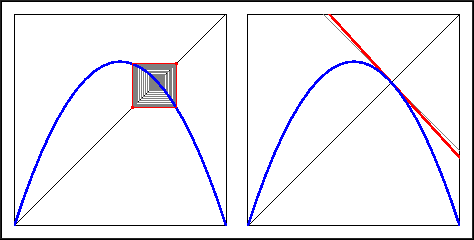
The fixed point other than 0 is repelling for
 = 3.1.
= 3.1.
For  = 3.1 the
graph of the derivative map no longer has a slope between -1 and
1. Hence, the fixed point is now repelling.
= 3.1 the
graph of the derivative map no longer has a slope between -1 and
1. Hence, the fixed point is now repelling.
 = 1.5
and 3.1?
= 1.5
and 3.1?
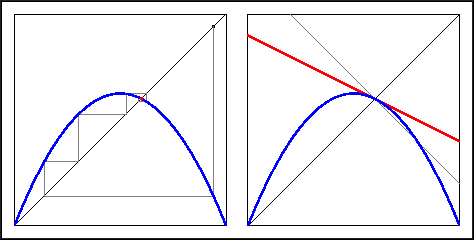
The fixed point other than 0 is attracting for
 = 2.5.
= 2.5.
 = 2.5 with
the figure for
= 2.5 with
the figure for
 = 1.5. Notice
the difference in behavior of the graphical iterations. Why do you
think this difference is there? (Hint: look at the slope of the graph
at the attracting fixed point.)
= 1.5. Notice
the difference in behavior of the graphical iterations. Why do you
think this difference is there? (Hint: look at the slope of the graph
at the attracting fixed point.)
Note: The procedure you found only works for periodic points with small periods. Although it is nice to have the condition above for whether a period-n point is attracting, it becomes computationally difficult to accurately graph the n-th iterate of a map as n becomes large.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Written by Hinke Osinga
Comments to:
webmaster@geom.umn.edu
Created: Apr 3 1998 ---
Last modified: Thu Apr 9 14:02:09 1998