Next: Logistic Growth Model
Up: Table of Contents
Prev: Introduction
One-Dimensional Dynamical Systems
Warm Up Questions
For these questions, you should first read the
Introduction. We start with an
exploration of linear dynamical systems. Later on you will learn how
(easy) linear systems help to explain the dynamics of (complicated)
nonlinear systems.
Let us consider the linear dynamical system
f(x) =
 x
x
as it was introduced in the
Introduction. For now, do not
think in terms of squirrels too much, both x and
 can be negative
numbers, and we accept non-integer values for them as well.
can be negative
numbers, and we accept non-integer values for them as well.
- The graph of f is simply a straight line. Draw the graphs
for
 = 0.1, 0.3, 1, 2,
and 5. Explain for each
= 0.1, 0.3, 1, 2,
and 5. Explain for each
 what the long term
behavior of the system is for arbitrary x. What happens for
x = 0? What happens for
what the long term
behavior of the system is for arbitrary x. What happens for
x = 0? What happens for
 = 1?
= 1?
Now look at the slope of each graph. Do you see a relation between the
long term behavior of the system and the slope of its graph?
- For negative
 the
graph of f is still a straight line. Draw the graphs for
the
graph of f is still a straight line. Draw the graphs for
 = -3, -1.8, -1, -0.5,
and -0.2. For each
= -3, -1.8, -1, -0.5,
and -0.2. For each  describe the long term behavior, and explain the difference in
behavior compared to positive
describe the long term behavior, and explain the difference in
behavior compared to positive
 .
.
Formulate the relation between the long term behavior of the system
and the slope of its graph, for both positive and negative slopes.
- In the above two exercises you have found two special lines,
corresponding to two special linear systems, namely
f(x) = x and
f(x) = -x.
Draw the graphs of these two functions. In the same picture sketch the
graph of a nonlinear function which is such that iterates of this
function go to infinity for all x
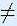 0.
0.
Make another picture with the graph of a nonlinear function whose
iterates go to 0 for all x.
To summarize the results:
The iterates of a linear system either go to 0 or to infinity, for
all x
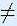 0.
0.
More complicated dynamics can only be obtained with nonlinear
dynamical systems. You should already be able to guess what the graph
of such a function needs to look like, in order to get different
dynamics. Let us consider nonlinear dynamical stystems that can be
found on your calculator.
- Suppose we have a dynamical system given by the square root
function on your calculator. Type in any number and calculate its
square root. Take the square root of the result. Take the square root
again and so on. Give a full description of the dynamics, similar to
what was done for the squirrel model. In particular, look for values
of x that do not change when taking the square root. Only
consider x
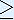 0.
0.
Draw the graph of the square root function, together with the two
special lines y = x and y = -x. What is special
about the points where the graph of the square root function
intersects one of the two lines?
- Give a description of the dynamics for a dynamical system given by
the cosine button, where x is given in radians.
Draw a graph of the cosine function for x given in
radians. Also draw the special lines y = x and y = -x.
Describe what is special about the points on the intersection
of the graph of the cosine function and these two lines.
Next: Logistic Growth Model
Up: Table of Contents
Prev: Introduction
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Written by Hinke Osinga
Comments to:
webmaster@geom.umn.edu
Created: Mar 31 1998 ---
Last modified: Fri Apr 10 15:11:11 1998
 x
x
 x
x
 can be negative
numbers, and we accept non-integer values for them as well.
can be negative
numbers, and we accept non-integer values for them as well.
 = 0.1, 0.3, 1, 2,
and 5. Explain for each
= 0.1, 0.3, 1, 2,
and 5. Explain for each
 what the long term
behavior of the system is for arbitrary x. What happens for
x = 0? What happens for
what the long term
behavior of the system is for arbitrary x. What happens for
x = 0? What happens for
 = 1?
= 1?
 the
graph of f is still a straight line. Draw the graphs for
the
graph of f is still a straight line. Draw the graphs for
 = -3, -1.8, -1, -0.5,
and -0.2. For each
= -3, -1.8, -1, -0.5,
and -0.2. For each  describe the long term behavior, and explain the difference in
behavior compared to positive
describe the long term behavior, and explain the difference in
behavior compared to positive
 .
.
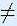 0.
0.
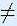 0.
0.
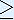 0.
0.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page