Next: Iteration
Up: Table of Contents
Prev: Warm Up Questions

One-Dimensional Dynamical Systems

Part 2: Logistic Growth Model

 The squirrel model in the introduction is called the exponential growth model. Suppose the current number of squirrels is p0, and pn denotes the number of squirrels after n years. Then we can construct the orbit p0, p1, p2, p3, ... by iterating

f(x) = lambdax.

We can even find an explicit formula for pn, namely:

pn = lambdan p0.

The name exponential growth model comes from the fact that n is in the exponent.

Nonlinear dynamics

We have derived a model for population growth,

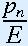pn+1 - pn = (lambda - 1) pn (1 - p_n over E).

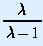that depends on a 'saturation' number E and the growth rate parameter lambda. If we substitute pn = E lambda over (lambda-1) xn, and write xn+1 = f(x) and xn = x, then the logistic growth model reduces to the simple dynamical system

f(x) = lambdax (1 - x).

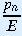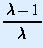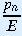Notice that the parameter E has disappeared. In fact, the variable x = p_n over E * (lambda-1) over lambda does not stand for the total number of squirrels in a specific year. We can think of x as representing a 'normalized' population. Since x is equal to p_n over E times a constant, it can be thought of as expressing the population of squirrels as a fraction of some adjusted saturation value.

Next: Iteration
Up: Table of Contents
Prev: Warm Up Questions
[HOME] The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 1 1998 --- Last modified: Wed Apr 8 18:19:53 1998