Up: Logistic Growth Model

One-Dimensional Dynamical Systems

Part 2: Logistic Growth Model

Visualizing an orbit

 Let us consider the evolution for p0 = 12, under the assumption that the university campus provides essential needs for maximally E = 200 squirrels. We set lambda = 2, which corresponds to a growth rate of 1 baby per squirrel each year. What do you expect to happen as the years go by? We can visualize the orbit of p0 = 12 by plotting the iterates pn against the years n. In the following picture the evolution is shown over 100 years.


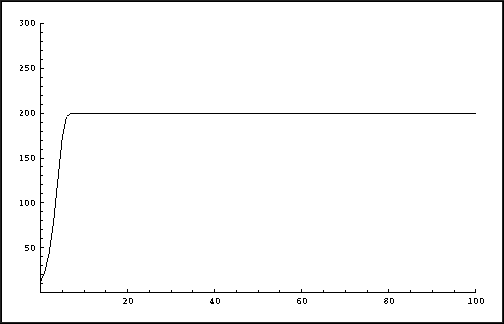
Logistic growth with growth factor lambda = 2.

The picture shows a monotonic increase towards the saturation value E. It is suprising to see what happens if we vary lambda, but still use E = 200 and p0 = 12. The following two pictures show the results over 100 years for lambda = 3.1 and lambda = 4. In the former case the population eventually oscillates between two different values. The latter case shows an unexpected, complicated behavior: chaos!


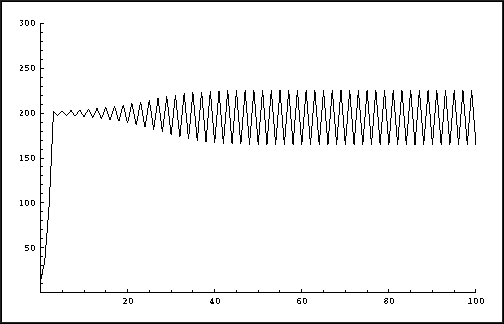
Logistic growth with growth factor lambda = 3.1.


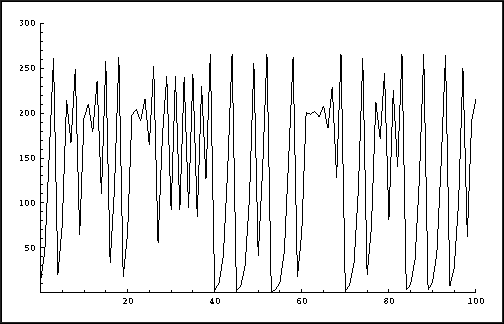
Logistic growth with growth factor lambda = 4.

Up: Logistic Growth Model
[HOME] The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 1 1998 --- Last modified: Wed Apr 8 18:10:03 1998