Up: Logistic Growth Model

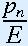One-Dimensional Dynamical Systems

Part 2: Logistic Growth Model

Derivation of the model

 The exponential growth model does not take into account the possibility that there may be finite resources. For an overcrowded population the growth rate should decrease, due to scarcity of food and other essentials. In a more realistic model we assume that the population only grows when the number of squirrels is less than a certain 'saturated' or equilibrium population E. The growth rate should decrease as the number of squirrels gets closer to E, and even become negative if the population grows larger than E. If the number of squirrels is exactly E, the population does not grow at all. We call E a fixed point (or equilibrium point) of our dynamical system. The new model looks like:

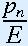pn+1 - pn = (lambda - 1) pn (1 - p_n over E).

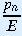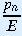The left hand side denotes the increase of the population from year n to year n+1. The term lambda - 1 is the growth rate, as given in the exponential growth model. If pn is a lot smaller than E, the term p_n over E is very small, and 1 - p_n over E is almost 1. Therefore, the right hand side is almost equal to (lambda - 1) pn, which means that there is still exponential growth. 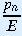However, if pn gets close to E, the term 1 - p_n over E tends to 0 and the population growth comes to a stop. The growth is exactly 0 when pn = E, and becomes negative as p becomes larger than E. Our new model is known as the logistic growth model.

Up: Logistic Growth Model
[HOME] The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 1 1998 --- Last modified: Wed Apr 8 18:08:57 1998