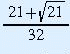 and
and
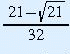 are period 2 points.
are period 2 points.
One-Dimensional Dynamical Systems
Part 4: Linear and Nonlinear Behavior
Periodic points
Recall that p is
a fixed point of f if f(p) =
p. This means that fixed points are the intersection points
of the graph of f and the diagonal y = x. This
observation makes it easy to find fixed points visually. If we want an
exact expression for the fixed point, we need to solve the
equation f(p) = p.
Let fn denote the n-th iterate of f. For example, f2(x) = f(f(x)) is the second iterate of x.
Definition(Periodic Point): We say that p is periodic with least period n, if fk(p) = p for k = n, and this is not true for any smaller value of k.
The orbit of a periodic point p with least period n consists of exactly n different points, since fk(p) = p. Saying "least period" all the time is cumbersome. Therefore, whenever we refer to a period n point, it is assumed to be of least period n.
For example, 1 is a fixed point of the function f(x) = 1/x, but 3 is mapped to 1/3 and 1/3 is mapped back to 3, so 3 is a periodic point of f(x) = 1/x, and its least period is 2. Note that 1/3 is then a periodic point of least period 2 as well.
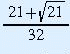 and
and
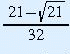 are period 2 points.
are period 2 points.
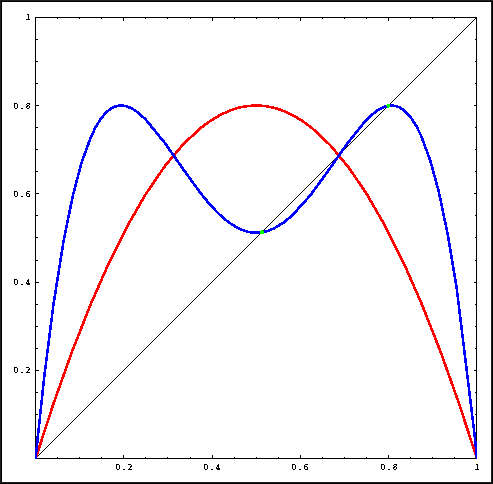
Points of period 2 for the Logistic map.
The method of finding fixed points graphically also works to find periodic points. For example, to find the points of least period two for a function f, look for the intersection points of the graph of f2 with the line y = x. The only catch is that fixed points are also period two points, but not of least period two. Thus you must first find the fixed points for f and discard them when looking at intersections of the graph of f2 and the line y = x.
For the following questions, read the instructions for the Macintosh or for other machines.
 = 3.2.
Check graphically the number of points of least period 2. Does this
agree with what you found above analytically?
= 3.2.
Check graphically the number of points of least period 2. Does this
agree with what you found above analytically?
 = 2, 3.2, and
3.5. Remember to exclude fixed points when you count intersections.
= 2, 3.2, and
3.5. Remember to exclude fixed points when you count intersections.
Just as with fixed points, periodic orbits can be attracting, repelling, or neutral. For a given periodic orbit, if orbits of nearby points converge to the periodic orbit, it is attracting. If orbits of nearby points move away from the periodic orbit, it is repelling. Otherwise it is neutral.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Written by Hinke Osinga
Comments to:
webmaster@geom.umn.edu
Created: Apr 3 1998 ---
Last modified: Thu Apr 9 13:49:41 1998