One-Dimensional Dynamical Systems

Part 4: Linear and Nonlinear Behavior

Eventual behavior

Let us investigate the Logistic family for lambda

= 3.2. Which of the fixed points are attracting? Which are repelling? What about the periodic points?

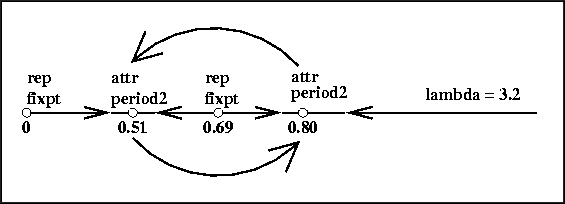
Qualitative diagram for = 3.2.

The above picture represents the eventual behavior of all points on the line for lambda = 3.2. With arrows we indicate that the two periodic points are mapped onto each other. For the other points, we use arrows to indicate the direction that points go after iteration. Note that a point x, close to one periodic point, will first be mapped close to the other periodic point before it gets mapped back to the line segment that contains x. This is not indicated in the picture, because this behavior is already reflected in the behavior of the periodic points themselves.

Draw a qualitative diagram for the eventual behavior of all points for = 2. Your diagram should resemble the picture above, but it does not need to have exact values for fixed and periodic points. The idea is to compare pictures qualitatively.
Draw a similar diagram for = 3.1. As you investigate, magnify the region near the fixed point other than 0. Compared to the behavior for = 2, what has happened?
Draw a similar diagram for = 3.5. What is the period of the attracting orbit here? Indicate in which order the points in the orbit occur.

Up: Linear and Nonlinear Behavior

The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 3 1998 --- Last modified: Wed Apr 8 19:26:13 1998