One-Dimensional Dynamical Systems

Part 4: Linear and Nonlinear Behavior

Instructions for Mathematica: Graphs of higher iterates

First make sure that you have a personal copy of the package Chaos.m.

To start up Mathematica in a Unix window, type 'math', or 'mathematica' if your prefer the notebook version. On a PC, use the start button and find Mathematica in the Program directory. The Package written for this course is called 'Chaos.m'. Inside Mathematica, load this Package by typing

<< Chaos.m

Instructions to graph higher iterates

Pick a value for and type lambda = .
Type PlotGraphical to get the graph of the corresponding function. If you do not want to see the graphical iteration, you can also type

ShowGraph[1, color]

where color is the color of the graph. You can choose: red, blue, green, yellow, pink, and purple, or RGBColor[a, b, c], with a, b, c in [0,1].
To add a graph of the second iterate to this picture, type

AddGraph[2, other-color]

You get a new picture that contains both graphs.
You may wish to zoom in to this picture. For this, type

Show[%, PlotRange -> {{0.6, 0.8}, {0.6, 0.8}}]

A new figure appears of only the box [0.6, 0.8] X [0.6, 0.8]. You can type something similar to zoom in more, but also to zoom out, even though the last picture does not show all points.

Instructions for Mathematica: Orbit Diagram

First make sure that you have a personal copy of the package Chaos.m.

<< Chaos.m

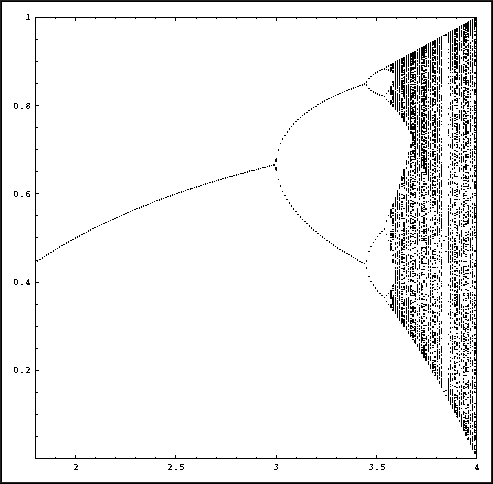
An enlargement of the orbit diagram for the Logistic family.

How to Study the Orbit Diagram

To start the computation, type

OrbitDiagram[first-its, total-its]

The program begins by computing total-its iterates of an arbitrary point x₀. However, iterates are displayed only after first-its iterates. Therefore, the transients are not shown in the picture. In Mathematica it is not possible to have the picture being partially drawn already while computing. Therefore, it may take quite a while. In total 200 orbits are computed for each picture, and a count-down is being printed so that you can guess how long it takes.
To get a picture that reflects the eventual attracting behavior more accurately, increase first-its and total-its.
You can zoom in with

Show[%, PlotRange -> {{3.1, 3.8}, {0.6, 0.8}}]

However, when you zoom in, you probably want to increase first-its and total-its even more. Therefore, you may want to type

OrbitDiagram[first-its, total-its, {{3.1, 3.8}, {0.6, 0.8}}]

The computations are done now only for the ranges specified. (So you cannot zoom out on this picture!)

Up: Linear and Nonlinear Behavior

The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 3 1998 --- Last modified: Mon May 11 16:35:21 1998