One-Dimensional Dynamical Systems

Part 5: Bifurcation

Orbit diagram

Now that you learned that a function can undergo bifurcations that change the qualitative dynamics, it is interesting to see how the dynamics really depends on the parameter. We want to visualize the relation between the dynamics of the Logistic map and the parameter lambda

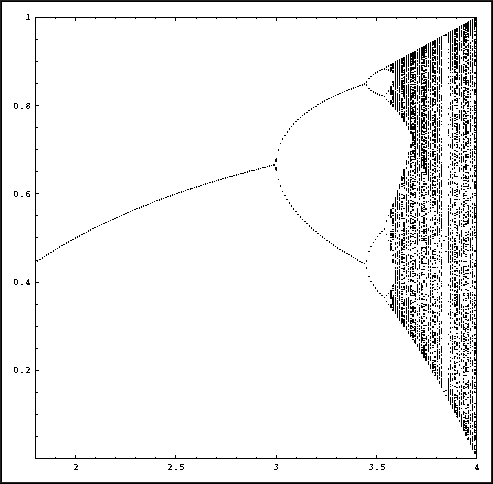
An enlargement of the orbit diagram for the Logistic family.

The picture above is called the orbit diagram for the Logistic family. It shows the eventual behavior of bounded orbits (that is, the orbits that do not just go off to infinity), as a function of the parameter. Question 3 from the homework asked you to make a partial sketch of this diagram. The values on the horizontal axis correspond to parameter values for lambda . The vertical values correspond to (eventual) iterates of an arbitrary point x₀. If the eventual behavior of x₀ is periodic, these iterates will repeat each other, and only a small number of points will be shown. For example, for lambda smaller than 3 there is only a single point for each value of lambda . This means that the orbit of x₀ goes to an (attracting) fixed point of the Logistic map.

Let the computer draw the orbit diagram and answer the questions below; see the instructions for the Macintosh or other machines.

At = 1 the curve suddenly turns away from the horizontal axis. What has happened?
Somewhere between 2 and 3.1, the orbit diagram curve splits into two branches. Why are there two branches now? What do they correspond to? (Hint: What was the eventual behavior of points in this region?)
Investigate further bifurcations as increases. Describe the sequence of bifurcations. In other words, how does the period of the attracting set change at each bifurcation?

Up: Bifurcation

The Geometry Center Home Page

Written by Hinke Osinga
Comments to: webmaster@geom.umn.edu
Created: Apr 6 1998 --- Last modified: Thu Apr 9 14:22:26 1998