
Conjectures in Geometry

An educational web site created for
high school geometry students
by
Jodi Crane, Linda Stevens, and Dave Wiggins
Introduction:
This site constitutes our final project for Math 5337-Computational Methods in Elementary Geometry, taken at the University of Minnesota's Geometry Center during Winter of 1996. This course could be entitled "Technology in the Geometry Classroom" as one of its more important objectives is to provide students (presumably math educators) with a wide variety of activities (demonstrations and assignments) utilizing computer software that could be incorporated into a high school geometry classroom.

This page has been designed to provide an interactive technological resource for students studying elementary high school geometry. Basic concepts, conjectures, and theorems found in typical geometry texts are introduced, explained, and investigated. Follow-up activities are provided to further demonstrate meanings and applications of concepts. The objective is to ensure that students develop a firm understanding of both the content and applications of each main idea given below in the list of conjectures.
Working towards this objective, we have included:
- Definitions of geometric terminology
- Sketches and explanations for each conjecture
- Interactive Geometer's Sketch Pad demonstrations of each conjecture
- Activities which help the student understand and apply the ideas from each conjecture towards solving typical geometric problems. Solutions are included.
- Links to Key Curriculum Press for demo versions of Geometer's Sketch Pad:

Twenty Conjectures in Geometry:

- Vertical Angle Conjecture: Non-adjacent angles formed by two intersecting lines.
- Linear Pair Conjecture: Adjacent angles formed by two intersecting lines.
- Triangle Sum Conjecture: Sum of the measures of the three angles in a triangle.
- Quadrilateral Sum Conjecture: Sum of the four angles in a convex four-sided figure.
- Polygon Sum Conjecture: Sum of the angles for any convex polygon.
- Exterior Angles Conjecture: Sum of exterior angles for any convex polygon.
- Isosceles Triangle Conjectures: Isosceles triangles have equal base angles.
- Isosceles Trapezoid Conjecture: Isosceles trapezoids have equal base angles.
- Midsegment Conjectures: Lengths of midsegments for triangles and trapezoids.
- Parallel Lines Conjectures: Corresponding, alternate interior, and alternate exterior angles.
- Parallelogram Conjectures: Side, angle, and diagonal relationships
- Rhombus Conjectures: Side, angle, and diagonal relationships.
- Rectangle Conjectures: Side, angle, and diagonal relationships.
- Congruent Chord Conjectures: Congruent chords intercept congruent arcs.
- Chord Bisector Conjecture: The bisector of a chord passes through the center of the circle.
- Tangents to Circles Conjectures: A tangent to a circle is perpendicular to the radius.
- Inscribed Angle Conjectures: An inscribed angles has half the measure of intercepted arc.
- Inscribed Quadrilateral Conjecture: Opposite angles are supplements.
- The Number "Pi" Conjectures: Circumference and diameter relationship for a circle.
- Arc Length Conjecture: Formula to calculate the length of an arc on a circle.

Organization of this Site:
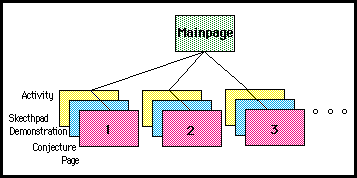
This site consists of:
- Main Page: This is the document you are reading now. It is linked directly to each of the twenty Conjecture Pages.
- Conjecture Pages: Each conjecture gets its own page. On this page, sketches and explanations will be given, as well as links to Geometer's Sketch Pad demonstrations and Worksheet Activities.
- Sketch Pad Demonstrations: Each conjecture is demonstrated through the use of Geometer's Sketch Pad
- Activity Work Sheets: Interested viewers are encouraged to visit the Activity Sheets that we have created for each conjecture. Activities include:
- Compass and straight edge constructions
- Geometer's Sketch Pad constructions
- Geometric problem solving using the main ideas from the conjecture
- Navigation Links: Each Conjecture and Activity Page is linked back to the Main Page. There are further links to "next" and "previous" Conjectures and Activities.

Sample High School Student Work
The students in Rob Rumppe's high school geometry class spent three class periods in the computer lab learning and working with Geometer's Sketch Pad. They performed investigations provided by Key Curriculm Press as support for the Sketch Pad software.
Please check out the discoveries they made while in the lab!!
Rob Rumppe is an innovative math educator (with multi-media interests) at Roosevelt High School in Minneapolis. Check him out!

Future Improvements:
In the future, we would like to expand this page to include:
- Link to a "Definitions Page" so students can look up terminology at the press of a button.
- More interactive Activity Sheets: developing Activity Sheets is a high priority for us right now. Presently, many are unfinished. Suggestions on how these can be made more interactive are welcome!
- Links to other interesting and educational Web Sites involving high school mathematics.
- More links to sites which illustrate work created by high school geometry students.
- Investigations and explanations of other geometric conjectures and formulas such as the Pythagorean Theorem, Areas, Volumes, similar triangles.
- Suggestions from readers like you. Please take the time to respond by e-mail to the authors below.
The shape of this page will be determined by the comments and suggestions of diligent viewers. If you see a need that we have not addressed, let us know. If there are topics you think should or should not be considered, by all means tell us. We are interested in making this a truly educational site.
Back to Conjecture List

References
This site drew heavily from the following sources:
- Key Curriculum Press: All pictures and sketches were created with Geometer's Sketch Pad.
- Discovering Geometry: An Inductive Approach, Michael Serra, Key Curriculum Press
- Geometry, Pearson and Lightner, Ginn and Company

Let us know what you think!!
If you have questions or comments about this page (especially typos!), please send e-mail to
jcrane@geom.umn.edu
lstevens@geom.umn.edu
dwiggins@math.umn.edu
Thank you for visiting our Geometric Conjecture site.
We hope it was both educational and useful for you!

We are in Search of Employment!!
For additional information about Dave Wiggins
For additional information about Jodi Crane
