Tangent Conjectures

Explanation:

A tangent line to a circle is any line which intersects the circle in exactly one point. You can think of a tangent line as "just touching" the circle, without ever traveling "inside". A line which intersects a circle in two points is called a secant line. Chords of a circle will lie on secant lines.

The precise statement of the conjecture is:

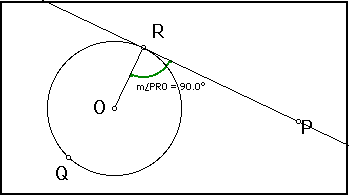
Conjecture (Tangent Conjecture I ): Any tangent line to a circle is perpendicular to the radius drawn to the point of tangency.

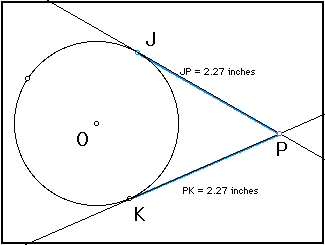
Conjecture (Tangent Conjecture II ): Tangent segments to a circle from a point outside the circle are equal in length.

Interactive Sketch Pad Demonstration:

Key Curriculum Press can provide demo versions of Geometer's Sketch Pad
- Sketchpad for Mac, Version 3.00 (721K)
- Sketchpad 3.04 for Windows (638K)
- More Sketch Pad download information
Linked Sketch Pad Demonstrations of the
- Tangent Conjecture I
- Tangent Conjecture II

Linked Activity:

Please feel free to try the activity sheet associated with this conjecture.

Next: Inscribed Angle Conjectures
Previous: Chord Bisector Conjecture
Back: Conjectures in Geometry Conjecture List or to the Introduction.