Quadrilateral Sum Conjecture

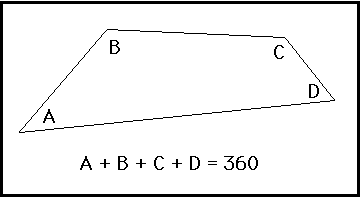
Explanation:

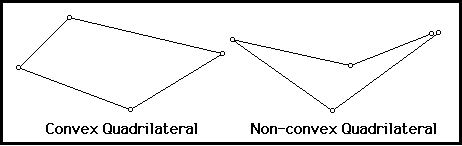
We have seen in the Triangle Sum Conjecture that the sum of the angles in any triangle is 180 degrees. The Quadrilateral Sum Conjecture tells us the sum of the angles in any convex quadrilateral is 360 degrees. Remember that a polygon is convex if each of its interior angles is less that 180 degree. In other words, the polygon is convex if it does not bend "inwards". The diagram below shows both convex and non-convex quadrilaterals.

The precise statement of the conjecture is:

Conjecture (Quadrilateral Sum ): The sum of the measures of the interior angles in any convex quadrilateral is 360 degrees.

Proof: The sum of the measures of the interior angles of any quadrilateral can be found by breaking the quadrilateral into two triangles. Since the measure of the interior angles of any triangle equals 180 degrees, each of the two triangles will contribute 180 degrees to the total for the quadrilateral.

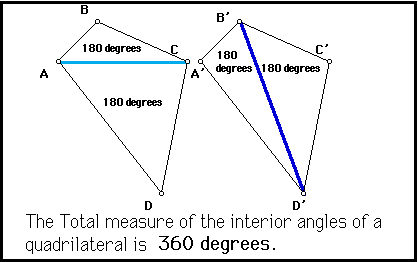
So the measure of the interior angles of a convex quadrilateral is the same as the sum of the measures of the interior angles of two triangles, or 360 degrees.

Question: What goes wrong if the quadrilateral is not convex?

Perhaps when you try the Sketch Pad demonstration, you will experiment with this question to find an answer!

Interactive Sketch Pad Demonstration:

Key Curriculum Press can provide demo versions of Geometer's Sketch Pad
- Sketchpad for Mac, Version 3.00 (721K)
- Sketchpad 3.04 for Windows (638K)
- More Sketch Pad download information
Linked Sketch Pad demonstration of this conjecture

Linked Activity:

Please feel free to try the activity sheet associated with this conjecture.

Next: Polygon Sum Conjecture
Previous: Triangle Sum Conjecture
Back: Conjectures in Geometry Conjecture List or to the Introduction.