Quadrilateral Sum Conjecture
Activity Sheet
The objectives for this activity sheet are:
- To determine your understanding of the Quadrilateral Sum Conjecture. Typical geometric problems requiring the ideas of this conjecture, coupled with ideas from previous conjectures, are given for you to solve.
- To give you the opportunity to explore this conjecture further through construction activities involving:
- Geometer's Sketch Pad
- Compass and Straight Edge
Solving Geometric Problems
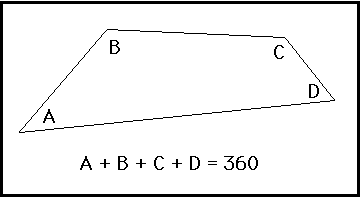
Use the Quadrilateral Sum Conjecture to find the missing values in the diagram below.
(Watch out! You may will the ideas from previous conjectures as well!!)
 solutions.
solutions.
Further Investigations with Geometer's Sketch Pad
Directions: Open the Geometer's Sketch Pad program on your computer. Then follow these directions:
- Construct a convex quadrilateral ABCD with four line segments: AB, BC, CD, and DA.
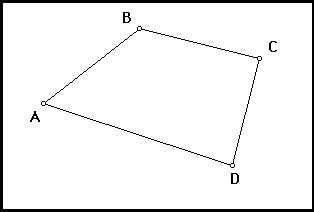
(Your sketch should look like this.)
- Measure each angle using the Measure Menu. Record each of these values.
- Angle ABC = ??
- Angle BCD = ??
- Angle CDA = ??
- Angle DAB = ??
- Add the measures of these four angles by selecting each of them, and using the Measure/Calculate Menu. What is the sum of their measures?
- Use the mouse to drag any of the vertices of the quadrilateral. Note what happens to the sum of the angle measurements.
- What happens?
- What happens if you drag a vertex so that the quadrilateral does not remain convex?
Are you convinced?
Compass and Straight Edge Activity
- Use a straight edge to construct any quadrilateral ABCD.
- Use a protractor to measure each of the four angles.
- Find the sum of the four angle measurements. What do you get?
- If you did not get a total of 360, what do you think happened?
- Try constructing another quadrilateral, perhaps one with a different shape to it. Measure each angle and find the total again.
- What do you get? Do you get 360? if not, are you close?
Are you convinced?
Back: Conjectures in Geometry home page or to the List of Conjectures.
Back: Explanation of the
Quadrilateral Sum Conjecture.
Next Conjecture: Explanation of the Polygon Sum Conjecture
Next Activity: Activities for Polygon Sum Conjecture
Solutions to Problems
- A = 87
- B = 93
- C = 140
- D = 20
- E = 120
- F = 60
- G = 67
- H = 65
- J = 67
- K = 113
- L = 120
- M = 77
- N = 60
Back to the Problem Set
solutions.