Polygon Sum Conjecture

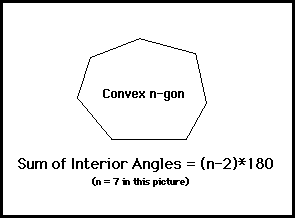
Explanation:

The idea is that any n-gon contains (n-2) non-overlapping triangles. (This is illustrated below for n = 6.) Then, since every triangle has angles which add up to 180 degrees (Triangle Sum Conjecture) each of the (n-2) triangles will contribute 180 degrees towards the total sum of the measures for the n-gon.

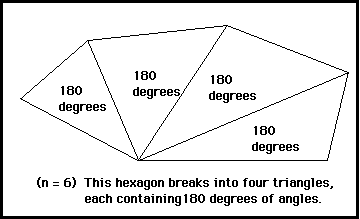For this hexagon, total is (6-2)*180 = 720

If you are still skeptical, then you can see for yourself. Below, you will find a linked Sketch Pad demonstration and activities which may help to change your mind!!

The precise statement of the conjecture is:

Conjecture (Polygon Sum Conjecture): The sum of the interior angles of any convex n-gon (polygon with n sides) is given by (n-2)*180.

Corollary (Angle Measures for Regular n-gons): The measure of each of the n angles in a regular n-gon is given by (n-2)*180/n.

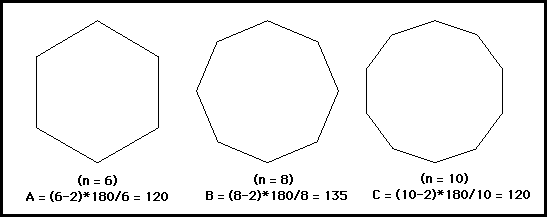
Explanation of the Corollary: By the Polynomial Sum Conjecture, the sum of the n angles is (n-2)*180 . Since each angle in a regular n-gon has equal measure, the measure must be equal to (n-2)*180 divided by n.

Interactive Sketch Pad Demonstrations:

Key Curriculum Press can provide demo versions of Geometer's Sketch Pad
- Sketchpad for Mac, Version 3.00 (721K)
- Sketchpad 3.04 for Windows (638K)
- More Sketch Pad download information
Linked Sketch Pad demonstration of this conjecture

Linked Activity:

Please feel free to try the activity sheet associated with this conjecture.

Next: Exterior Angles Conjecture
Previous: Quadrilateral Sum Conjecture
Back: Conjectures in Geometry Conjecture List or to the Introduction.