
Arc Length Conjecture

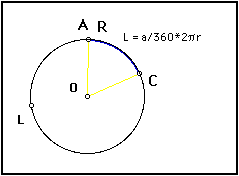
Explanation:
The arc length of a circle is the distance from one point on the circumference to another point on the circumference, "traveling" along the edge of the circle. Because we know that the measure of the central angle is equal to the arc it intercepts, (Inscribed angle conjectures) by dividing that measure by 360 degrees, we find out what fraction of the circumference that the arc covers.
The precise statement of the conjecture is:
Conjecture (Arc Length ):
The arc length of an arc on a circle is given by
L = m/360 degrees * circumference
where m is the measure of the central angle.
Interactive Sketch Pad Demonstration:
Linked Activity:
Please feel free to try the activity sheet associated with this conjecture.
Next: Back to the main page
Previous: Circumference and "Pi" conjecture
Back: Conjectures in Geometry Conjecture List or to the Introduction.



