
Parallelogram Conjectures

Explanation:
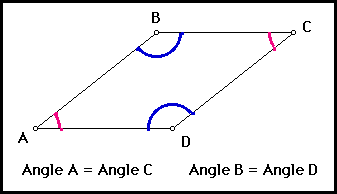
A parallelogram is a quadrilateral with two pairs of parallel sides. If we extend the sides of the parallelogram in both directions, we now have two parallel lines cut by two parallel transversals. The parallel line conjectures will help us to understand that the opposite angles in a parallelogram are equal in measure. When two parallel lines are cut by a transversal corresponding angles are equal in measure. Also, the vertical angles are equal in measure. Now we need to extend our knowledge to two parallel lines cut by two parallel transversals. We have new pairs of corresponding angles.
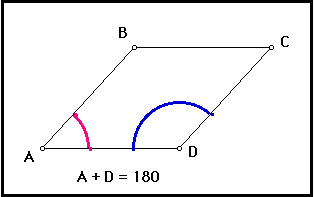
What can be said about the adjacent angles of a parallelogram. Again the parallel line conjectures and linear pairs conjecture can help us. The measures of the adjacent angles of a parallelogram add up to be 180 degrees, or they are supplementary.
The precise statement of the conjectures are:
Conjecture (Parallelogram Conjecture I ):
Opposite angles in a parallelogram are congruent.

Conjecture (Parallelogram Conjecture II ):
Adjacent angles in a parallelogram are supplementary.

Conjecture (Parallelogram Conjecture III ):
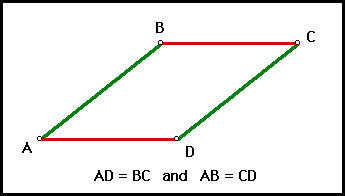
Opposite sides of a parallelogram are equal in length.

Conjecture (Parallelogram Conjecture IV ):
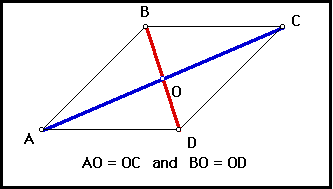
The diagonals of a parallelogram are bisected by the point of their intersection.

Interactive Sketch Pad Demonstration:
- Key Curriculum Press can provide demo versions of Geometer's Sketch Pad
- Linked Sketch Pad Demonstrations of the
Linked Activity:
Please feel free to try the activity sheet associated with these conjectures.
Next: Rhombus Conjectures
Previous: Parallel Lines Conjectures
Back: Conjectures in Geometry Conjecture List or to the Introduction.



