Parallel Lines Conjectures

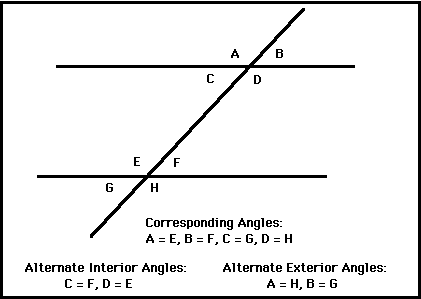
Explanation:

A line passing through two or more other lines in a plane is called a transversal. A transversal intersecting two parallel lines creates three different types of angle pairs. They are:

corresponding angles
alternate interior angles
alternate exterior angles

The precise statement of the conjecture is:

Conjecture (Corresponding Angles Conjecture ): If two parallel lines are cut by a transversal, the corresponding angles are congruent.

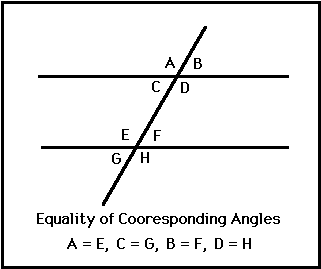
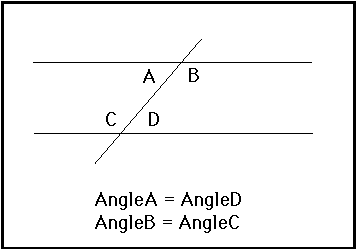
Conjecture (Alternate Interior Angles Conjecture ): If two parallel lines are cut by a transversal, the alternate interior angles are congruent.

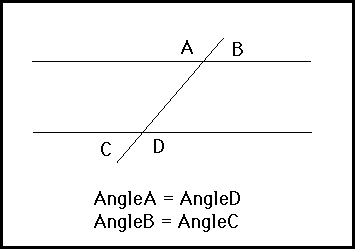
Conjecture (Alternate Exterior Angles Conjecture ): If two parallel lines are cut by a transversal, the corresponding angles are congruent.

Interactive Sketch Pad Demonstration:

Key Curriculum Press can provide demo versions of Geometer's Sketch Pad
- Sketchpad for Mac, Version 3.00 (721K)
- Sketchpad 3.04 for Windows (638K)
- More Sketch Pad download information
Linked Sketch Pad Demo of the

Linked Activity:

Please feel free to try the activity sheet associated with this conjecture.

Next: Parallelogram Conjectures
Previous: Midsegment Conjectures
Back: Conjectures in Geometry Conjecture List or to the Introduction.