Congruent Chords Conjecture

Explanation:

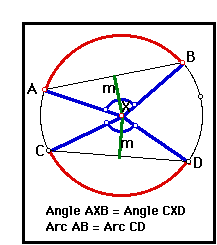
A chord is a line segment with endpoints on the circle. We want to know when two chords in a circle are congruent. This conjecture tells us that the central angles determined by the congruent chords are equal in measure, which implies that the intercepted arcs are congruent. This conjectures also tells us that the distances from the center of the circle to two congruent chords are equal.

The precise statement of the conjecture is:

Conjecture (Congruent Chords ):

If two chords of a circle are congruent, then they determine central angles which are equal in measure.

If two chords of a circle are congruent, then their intercepted arcs are congruent.

Two congruent chords in a circle are equal in distance from the center.

Interactive Sketch Pad Demonstration:

Key Curriculum Press can provide demo versions of Geometer's Sketch Pad
- Sketchpad for Mac, Version 3.00 (721K)
- Sketchpad 3.04 for Windows (638K)
- More Sketch Pad download information
Linked Sketch Pad demonstration of the Congruent Chords Conjecture

Linked Activity:

Please feel free to try the activity sheet associated with this conjecture.

Next: Perpendicular Bisector of a Chord
Previous: Rectangle Conjectures
Back: Conjectures in Geometry Conjecture List or to the Introduction.