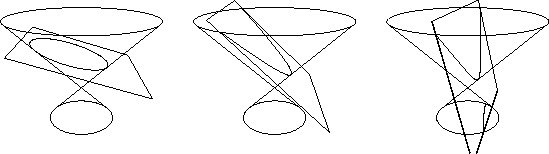
Figure 1: Left: A section of a cone by a plane can yield an ellipse (left), a parabola (middle) or a hyperbola (right).
Next: 7.1 Alternative Characterization
Up: Part I: Two-Dimensional Geometry
Previous: 6 Circles
A conic (or conic section) is a plane curve that can be obtained by intersecting a cone (Section 13.3) with a plane that does not go through the vertex of the cone. There are three possibilities, depending on the relative position of the cone and the plane (Figure 1). If no line of the cone is parallel to the plane, the intersection is a closed curve, called an ellipse. If one line of the cone is parallel to the plane, the intersection is an open curve whose two ends are asymptotically parallel; this is called a parabola. Finally, there may be two lines in the cone parallel to the plane; the curve in this case has two open pieces, and is called a hyperbola.

Figure 1: Left: A section of a cone by a plane can yield an ellipse
(left), a parabola (middle) or a hyperbola (right).
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.