 0).
0).
Next: 7.2 The General Quadratic Equation
Up: 7 Conics
Previous: 7 Conics
Assume given a point F in the plane, a line d not going through
F, and a positive real number e. The set of points P such that
the distance PF is e times the distance from P to d (measured
along a perpendicular) is a conic. We call F the focus, d
the directrix and e the eccentricity of the conic. If e<1 we
have an ellipse, if e=1 a parabola, and if e>1 a hyperbola
(Figure 1). This construction gives all conics
except the circle, which is a particular case of the ellipse according
to the earlier definition (we can recover it by taking the limit
e 0).
0).
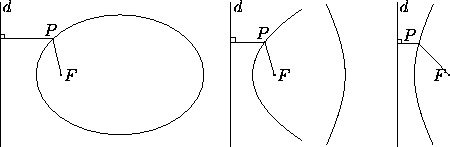
Figure 1: Left: Definition of conics by means of the ratio
(eccentricity) between the distance to a point and the distance to a
line. On the left, e=.7; on the middle, e=1; on the right, e=2.
For any conic, a line perpendicular to d and passing through F is an axis of symmetry. The ellipse and the hyperbola have an additional axis of symmetry, perpendicular to the first, so there is an alternate focus and directrix F' and d' obtained as the reflection of F and d with respect to this axis. (By contrast, the focus and directrix are uniquely defined for a parabola.)
The simplest analytic form for the ellipse and hyperbola is obtained when the two symmetry axes coincide with the coordinate axes. The ellipse in Figure 2 has equation
with b<a. The x-axis is the major axis, and the y-axis is
the minor axis. These names are also applied to the segments
determined on the axes by the ellipse, and to the lengths of these
segments: 2a for the major axis and 2b for the minor. The
vertices are the intersections of the major axis with the
ellipse, and have coordinates (a,0) and (-a,0). The distance from
the center to either focus is 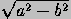 , and the sum of
the distances from a point in the ellipse to the foci is 2a. The
latera recta (in the singular, latus rectum) are the chords
perpendicular to the major axis and going through the foci; their
length is 2b
, and the sum of
the distances from a point in the ellipse to the foci is 2a. The
latera recta (in the singular, latus rectum) are the chords
perpendicular to the major axis and going through the foci; their
length is 2b /a. The eccentricity is
/a. The eccentricity is 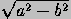 /a. All
ellipses of the same eccentricity are similar; in other words, the
shape of an ellipse depends only on the ratio b/a. The distance
from the center to either directrix is a
/a. All
ellipses of the same eccentricity are similar; in other words, the
shape of an ellipse depends only on the ratio b/a. The distance
from the center to either directrix is a /
/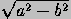 .
.
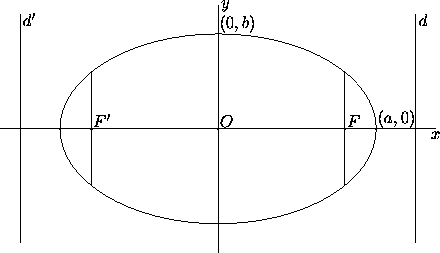
Figure 2: Left: Ellipse with major semiaxis a and minor semiaxis b.
Here b/a=0.6.
The hyperbola in Figure 3 has equation
The x-axis is the transverse axis, and the y-axis is the
conjugate axis. The vertices are the intersections of the
transverse axis with the ellipse, and have coordinates (a,0) and
(-a,0). The segment thus determined, and its length 2a, is also
called the transverse axis, while the length 2b is also called the
conjugate axis. The distance from the center to either focus is
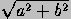 , and the difference between the distances from a
point in the hyperbola to the foci is 2a. The latera recta are
the chords perpendicular to the transverse axis and going through the
foci; their length is 2b
, and the difference between the distances from a
point in the hyperbola to the foci is 2a. The latera recta are
the chords perpendicular to the transverse axis and going through the
foci; their length is 2b /a. The eccentricity is
/a. The eccentricity is
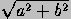 /a. The distance from the center to either
directrix is a
/a. The distance from the center to either
directrix is a /
/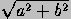 . The legs of the hyperbola
approach the asymptotes, lines of slope ±b/a that cross at
the center.
. The legs of the hyperbola
approach the asymptotes, lines of slope ±b/a that cross at
the center.
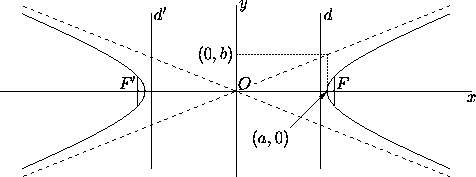
Figure 3: Left: Hyperbola with transverse semiaxis a and conjugate
semiaxis b.
Here b/a=0.4.
All hyperbolas of the same eccentricity are similar; in other words,
the shape of a hyperbola depends only on the ratio b/a. Unlike the
case of the ellipse (where the major axis, containing the foci, is
always longer than the minor axis), the two axes of a hyperbola can
have arbitrary lengths. When they have the same length, so that
a=b, the asymptotes are perpendicular, and e=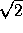 , the hyperbola
is called rectangular.
, the hyperbola
is called rectangular.
The simplest analytic form for the parabola is obtained when the symmetry axis coincides with one coordinate axis and the vertex (the intersection of the axis with the curve) is at the origin. The parabola on the right has equation
where a is the distance from the vertex to the focus, or, which is the same, from the vertex to the directrix. The latus rectum is the chord perpendicular to the axis and going through the focus; its length is 4a. All parabolas are similar: they can be made to look identical by scaling, translation and rotation.
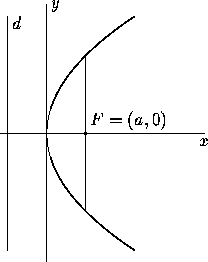
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.