
Next: 7.3 Additional Properties of Ellipses
Up: 7 Conics
Previous: 7.1 Alternative Characterization
The analytic equation for a conic in arbitrary position is the following:
where at least one of A, B, C is nonzero. To reduce this to one of the forms given previously, perform the following steps (note that the decisions are based on the most recent values of the coefficients, taken after all the transformations so far):
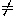 0, simultaneously perform the substitutions x
0, simultaneously perform the substitutions x qx+y and
y
qx+y and
y qy-x, where
qy-x, where
Now C=0. (This step corresponds to rotating and scaling about the origin.)
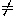 0.
0.
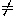 0, perform the substitution y
0, perform the substitution y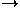 y-½(E/B). (This
corresponds to translating in the y direction.)
Now E=0.
y-½(E/B). (This
corresponds to translating in the y direction.)
Now E=0.
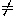 0, perform the substitution x
0, perform the substitution x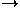 x-(F/D)
(translation in the x direction) and divide the
equation by B to get (3)
. The conic is a parabola.
x-(F/D)
(translation in the x direction) and divide the
equation by B to get (3)
. The conic is a parabola.
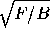 . If F>0 we have two imaginary
lines; the equation has no solution over the real numbers.
. If F>0 we have two imaginary
lines; the equation has no solution over the real numbers.
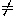 0:
0:
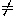 0, perform the substitution x
0, perform the substitution x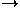 x-½(D/A).
Now D=0.
(This
corresponds to translating in the x direction.)
x-½(D/A).
Now D=0.
(This
corresponds to translating in the x direction.)
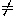 0, divide the equation by F to get a form with F=1.
0, divide the equation by F to get a form with F=1.
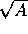 and b=1/
and b=1/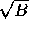 .
.
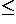 B, then make a=1/
B, then make a=1/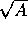 and b=1/
and b=1/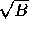 . The circle is the
particular case a=b.
. The circle is the
particular case a=b.
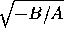 x, and when they have the same sign we get a point
(the origin).
x, and when they have the same sign we get a point
(the origin).
We work out an example for clarity. Suppose the original equation is
In step 1 we apply the substitutions x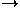 2x+y and
y
2x+y and
y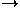 2y-x. This gives 25x
2y-x. This gives 25x +10x-5y+1=0. Next we interchange x
and y (step 2) and get 25y
+10x-5y+1=0. Next we interchange x
and y (step 2) and get 25y +10y-5x+1=0.
Replacing y by y-
+10y-5x+1=0.
Replacing y by y-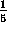 in step 3 we get
25y
in step 3 we get
25y -5x=0. Finally, in step 4a we divide the equation
by 25, thus giving it the form (3)
with a=
-5x=0. Finally, in step 4a we divide the equation
by 25, thus giving it the form (3)
with a=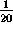 .
We have reduced the conic to a parabola with vertex at the origin and
focus at (
.
We have reduced the conic to a parabola with vertex at the origin and
focus at (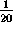 ,0). To locate the features of the original
curve, we work our way back along the chain of substitutions (recall
the convention about substitutions and transformations from
Section 1.1):
,0). To locate the features of the original
curve, we work our way back along the chain of substitutions (recall
the convention about substitutions and transformations from
Section 1.1):
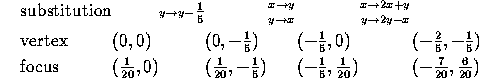
We conclude that the original curve (3)
is a parabola with
vertex 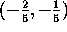 and focus
and focus 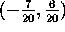 .
.
If one just wants to know the type of the conic defined by (1) , an alternative analysis consists in forming the quantities
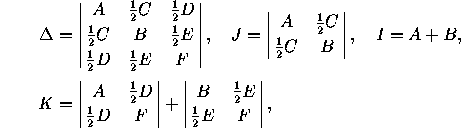
and finding the appropriate case in the following table, where an entry in parentheses indicates that the equation has no solution over the real numbers:

For the central conics (the ellipse, the point, and the hyperbola),
the center (x ,y
,y ) is the solution of the system of equations
) is the solution of the system of equations
2Ax+Cy+D=0,
Cx+2By+E=0,
and the axes have slope q and -1/q, where q is given by (2) .
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.