 /a
/a +y
+y /b
/b =1, with a>b,
and let F,F'=(±
=1, with a>b,
and let F,F'=(±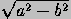 ,0) be its foci (see
Figure 7.1.2
).
,0) be its foci (see
Figure 7.1.2
).
Next: 7.4 Additional Properties of Hyperbolas
Up: 7 Conics
Previous: 7.2 The General Quadratic Equation
Let C be the ellipse with equation x /a
/a +y
+y /b
/b =1, with a>b,
and let F,F'=(±
=1, with a>b,
and let F,F'=(±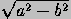 ,0) be its foci (see
Figure 7.1.2
).
,0) be its foci (see
Figure 7.1.2
).
(a cos  , b sin
, b sin  ).
).
The area of the shaded sector below is
½ab =½ab arccos(x/a).
=½ab arccos(x/a).
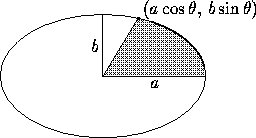
The length
of the arc from (a,0) to the point (a cos  , b sin
, b sin  )
is given by
a( E(pi/2,e) - E(pi/2 - theta, e) ), where E is an elliptic integral
(see the
Standard Math Tables and Formulas
for elliptic integrals). Setting
)
is given by
a( E(pi/2,e) - E(pi/2 - theta, e) ), where E is an elliptic integral
(see the
Standard Math Tables and Formulas
for elliptic integrals). Setting  =2
=2 we get
we get
area C= ab,
ab,
perimeter C=4a E(pi/2,e).
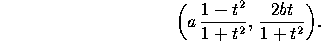
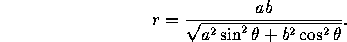
With respect to a coordinate system with origin at a focus, the equation is

where l=b /a is half the latus rectum. (Use the +
sign for the focus with positive x-coordinate and the - sign for
the other.)
/a is half the latus rectum. (Use the +
sign for the focus with positive x-coordinate and the - sign for
the other.)
 .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.