Next: 7.5 Additional Properties of Parabolas
Up: 7 Conics
Previous: 7.3 Additional Properties of Ellipses
Let C be the hyperbola with equation x /a
/a -y
-y /b
/b =1, and let
F,F'=(±
=1, and let
F,F'=(±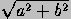 ,0) be its foci (see
Figure 7.1.3
). The conjugate hyperbola of C is
the hyperbola C' with equation -x
,0) be its foci (see
Figure 7.1.3
). The conjugate hyperbola of C is
the hyperbola C' with equation -x /a
/a +y
+y /b
/b =1. It has the same
asymptotes as C, the same axes (transverse and conjugate axes being
interchanged), and its eccentricity e' is related to that of C by
1/e'
=1. It has the same
asymptotes as C, the same axes (transverse and conjugate axes being
interchanged), and its eccentricity e' is related to that of C by
1/e' +1/e
+1/e =1.
=1.
- A parametric representation for C is
(a sec
 , b tan
, b tan  ).
).
A different parametric
representation, which gives one branch only, is
(a cosh  , b sinh
, b sinh  ):
):
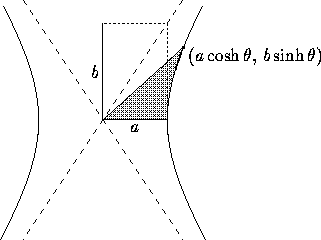
The area of the shaded sector above is
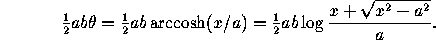
The length
of the arc from (a,0) to the point
(a cosh  , b sinh
, b sinh  )
)
is given by the elliptic integral
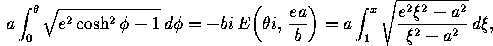
where e is the eccentricity, 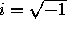 , and x=a cosh
, and x=a cosh  .
(See the
Standard Math Tables and Formulas
for elliptic integrals.)
.
(See the
Standard Math Tables and Formulas
for elliptic integrals.)
- A rational parametric representation for C is given by
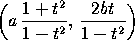 .
.
- The polar equation for C in the usual polar coordinate system is
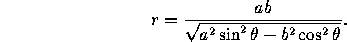
With respect to a system with origin at a focus the equation is

where l=b /a is half the latus rectum. (Use the - sign for the
focus with positive x-coordinate and the + sign for the other.)
/a is half the latus rectum. (Use the - sign for the
focus with positive x-coordinate and the + sign for the other.)
- Let P be any point of C. The unsigned difference between the
distances PF and PF' is constant, and equal to 2a.
- Let P be any point of C. Then the rays PF and PF' make the
same angle with the tangent to C at P. Thus any light ray
originating at F and reflected in the hyperbola will appear to
emanate from F'.
- Let T be any line tangent to C. The product of the distances
from F and F' to T is constant, and equals b
 .
.
- Let P be any point of C. The area of the parallelogram formed by
the asymptotes and the parallels to the asymptotes going through P
is constant, and equals ½ab.
- Let L be any line in the plane. If L intersects C at P and
P', and intersects the asymptotes at Q and Q', the distances
PQ and P'Q' are the same. If L is tangent to C we have
P=P', so the point of tangency bisects the segment QQ'.
Next: 7.5 Additional Properties of Parabolas
Up: 7 Conics
Previous: 7.3 Additional Properties of Ellipses
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
 /a
/a -y
-y /b
/b =1, and let
F,F'=(±
=1, and let
F,F'=(±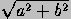 ,0) be its foci (see
Figure 7.1.3
). The conjugate hyperbola of C is
the hyperbola C' with equation -x
,0) be its foci (see
Figure 7.1.3
). The conjugate hyperbola of C is
the hyperbola C' with equation -x /a
/a +y
+y /b
/b =1. It has the same
asymptotes as C, the same axes (transverse and conjugate axes being
interchanged), and its eccentricity e' is related to that of C by
1/e'
=1. It has the same
asymptotes as C, the same axes (transverse and conjugate axes being
interchanged), and its eccentricity e' is related to that of C by
1/e' +1/e
+1/e =1.
=1.
 , b tan
, b tan 
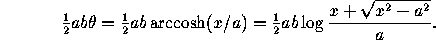
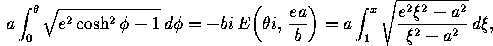
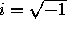 , and x=a cosh
, and x=a cosh 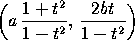 .
.
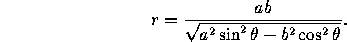

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page