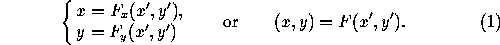
Next: 1.2 Cartesian Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1 Coordinate Systems in the Plane
Formulas for changes in coordinate systems can lead to confusion because (for example) moving the coordinate axes up has the same effect on equations as moving objects down while the axes stay fixed. (To read the next paragraph, you can move your eyes down or slide the page up.)
To avoid confusion, we will carefully distinguish between transformations of the plane and substitutions, as explained below. Similar considerations will apply to transformations and substitutions in three dimensions (see Section 9.1).
A substitution, or change of coordinates, relates the coordinates of a point in one coordinate system to those of the same point in a different coordinate system. Usually one coordinate system has the superscript ' and the other does not, and we write
This means: given the equation of an object in the unprimed coordinate
system, one obtains the equation of the same object in the
primed coordinate system by substituting F (x',y') for x and
F
(x',y') for x and
F (x',y') for y in the equation. For instance, suppose the
primed coordinate system is obtained from the unprimed system by
moving the axes up a distance d. Then x=x' and y=y'+d. The
circle with equation x
(x',y') for y in the equation. For instance, suppose the
primed coordinate system is obtained from the unprimed system by
moving the axes up a distance d. Then x=x' and y=y'+d. The
circle with equation x +y
+y =1 in the unprimed system has equation
x'
=1 in the unprimed system has equation
x' +(y'+d)
+(y'+d) =1 in the primed system. Thus transforming an implicit
equation in (x,y) into one in (x',y') is immediate.
=1 in the primed system. Thus transforming an implicit
equation in (x,y) into one in (x',y') is immediate.
The point P=(a,b) in the unprimed system, with equation x=a,
y=b, has equation F (x',y')=a, F
(x',y')=a, F (x',y')=b in the new system.
To get the primed coordinates explicitly one must solve for x' and
y' (in the example just given we have x'=a, y'+d=b, which yields
x'=a, y'=b-d). Therefore if possible we give the inverse
equations
(x',y')=b in the new system.
To get the primed coordinates explicitly one must solve for x' and
y' (in the example just given we have x'=a, y'+d=b, which yields
x'=a, y'=b-d). Therefore if possible we give the inverse
equations
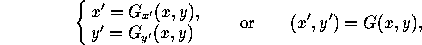
which are equivalent to (1) if G(F(x,y))=(x,y) and F(G(x,y))=(x,y). Then to go from the unprimed to the unprimed system one merely plugs the known values of x and y into these equations. This is also the best strategy when dealing with a curve expressed parametrically, that is: x=x(t), y=y(t).
A transformation associates to each point (x,y) a different point in the same coordinate system; we denote this by
where F is a map from the plane to itself (a two-component function
of two variables). For example, translating down by a distance d is
accomplished by (x,y) (x, y-d) (Section 2).
Thus the action of the transformation on a
point whose coordinates are known (or on a curve expressed
parametrically) can be immediately computed.
(x, y-d) (Section 2).
Thus the action of the transformation on a
point whose coordinates are known (or on a curve expressed
parametrically) can be immediately computed.
If, on the other hand, we have an object (say a curve) defined implicitly by the equation C(x,y)=0, finding the equation of the transformed object requires using the inverse transformation
(x,y) G(x,y)
G(x,y)
defined by G(F(x,y))=(x,y) and F(G(x,y))=(x,y). The equation of
the transformed object is C(G(x,y))=0. For instance, if C is the
circle with equation x +y
+y =1 and we are translating down by a
distance d, the inverse transformation is
=1 and we are translating down by a
distance d, the inverse transformation is
(x,y) (x, y+d)
(x, y+d)
(translating up), and the equation of the translated circle is
x +(y+d)
+(y+d) =1. Compare the example following (1)
.
=1. Compare the example following (1)
.
Usually, we will not give formulas of the form (1) for changes between two coordinate systems of the same type, because they can be immediately derived from the corresponding formulas (2) for transformations, which are given here (Section 2). We give two examples for clarity.
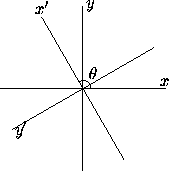
Figure 1:
Change of coordinates by a rotation.
Let the two cartesian coordinate systems (x,y) and (x',y') be
related as follows (Figure 1): they have the same origin, and the positive
x'-axis is obtained from the positive x-axis by a
(counterclockwise) rotation through an angle  .
If a point has coordinates (x,y) in the
unprimed system, its coordinates (x',y') in the primed system are
the same as the coordinates in the unprimed system of a point that
undergoes the inverse rotation, that is, a rotation by an angle
.
If a point has coordinates (x,y) in the
unprimed system, its coordinates (x',y') in the primed system are
the same as the coordinates in the unprimed system of a point that
undergoes the inverse rotation, that is, a rotation by an angle
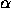 =-
=- . According to (2.1.1)
, this
transformation acts as follows:
. According to (2.1.1)
, this
transformation acts as follows:
Therefore the right-hand side of (3) is (x',y'), and the desired substitution is
x' = x cos  + y sin
+ y sin  ,
,
y' = -x sin  + y cos
+ y cos  .
.
Switching the roles of the primed and unprimed systems we get the equivalent substitution
x' = x cos  + -y sin
+ -y sin  ,
,
y' = x sin  + y cos
+ y cos 
(since the x-axis is obtained from the x'-axis by a
rotation through an angle - ).
).
Similarly,
let the two cartesian coordinate systems (x,y) and
(x',y') differ by a translation: x is parallel to x' and y to
y', and the origin of the second system coincides with the point
(x ,y
,y ) of the first system.
The coordinates
(x,y) and (x',y') of a point are related by
) of the first system.
The coordinates
(x,y) and (x',y') of a point are related by
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.