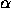 around a point P;
around a point P;
Next: 2.1 Formulas for Symmetries in Cartesian Coordinates
Up: Part I: Two-Dimensional Geometry
Previous: 1.5 Oblique Coordinates in the Plane
A transformation of the plane (invertible map of the plane to itself) that preserves distances is called an isometry of the plane. Every isometry of the plane is of one of the following types:
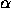 around a point P;
around a point P;
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.