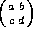 (x,y)=(ax+by, cx+dy).
(x,y)=(ax+by, cx+dy).
Next: 2.2 Formulas for Symmetries in Homogeneous Coordinates
Up: 2 Plane Symmetries or Isometries
Previous: 2 Plane Symmetries or Isometries
In the formulas below, a multiplication between a matrix and a pair of
coordinates should be carried out regarding the pair as a column
vector (or a matrix with two rows and one column). Thus
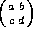 (x,y)=(ax+by, cx+dy).
(x,y)=(ax+by, cx+dy).
Translation by (x ,y
,y ):
):
(x,y) (x+x
(x+x , y+y
, y+y )
)
Rotation through 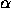 (counterclockwise) around the origin:
(counterclockwise) around the origin:
Rotation through 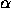 (counterclockwise)
around an arbitrary point (x
(counterclockwise)
around an arbitrary point (x ,y
,y ):
):
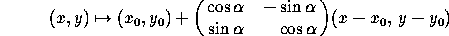
Reflection in the x-axis:
(x,y) (x,-y)
(x,-y)
Reflection in the y-axis:
(x,y) (-x,y)
(-x,y)
Reflection in the xy-diagonal:
(x,y) (y,x)
(y,x)
Reflection in a line with equation ax+by+c=0:
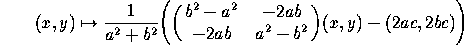
Reflection in a line going through (x ,y
,y ) and making an
angle
) and making an
angle 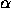 with the x-axis:
with the x-axis:
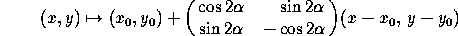
Glide-reflection in a line L with displacement d: Apply first a reflection in L, then a translation by a vector of length d in the direction of L, that is, by the vector

if L has equation ax+by+c=0.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.