 ,y
,y ):
):
Next: 2.3 Formulas for Symmetries in Polar Coordinates
Up: 2 Plane Symmetries or Isometries
Previous: 2.1 Formulas for Symmetries in Cartesian Coordinates
All isometries of the plane can be expressed in homogeneous coordinates in terms of multiplication by a matrix. This fact is useful in the implementation of these transformations on the computer, for example. It also means that the successive application of transformations reduces to matrix multiplication. The corresponding matrices are as follows:
Translation by (x ,y
,y ):
):
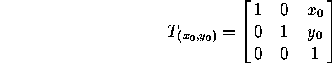
Rotation through 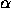 around the origin:
around the origin:
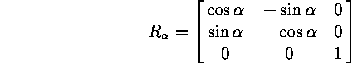
Reflection in a line going
through the origin and making an angle 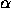 with the x-axis:
with the x-axis:
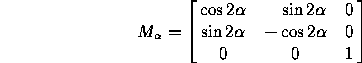
From this one can deduce all other transformations: for example, to
find the matrix for a rotation through 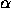 around an arbitrary
point P=(x
around an arbitrary
point P=(x ,y
,y ), we apply a translation by -(x
), we apply a translation by -(x ,y
,y ) to move
P to the origin, then a rotation through
) to move
P to the origin, then a rotation through 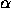 around the origin,
then a translation by (x
around the origin,
then a translation by (x ,y
,y ):
):
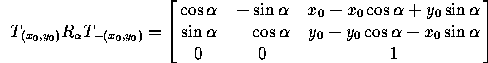
(notice the order of the multiplication).
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.