Next: 1.3 Polar Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1.1 Substitutions and Transformations
In cartesian coordinates (or rectangular coordinates), the
``address'' of a point P is given by two real numbers indicating the
positions of the perpendicular projections from the point to two
fixed, perpendicular, graduated lines, called the axes. If one
coordinate is denoted x and the other y, the axes are called the
x-axis and the y-axis, and we write P=(x,y). Usually
the x-axis is drawn horizontal, with x increasing to the right,
and the y-axis is drawn vertical, with y increasing going up. The
point x=0, y=0 is the origin, where the axes intersect.
See Figure 1.
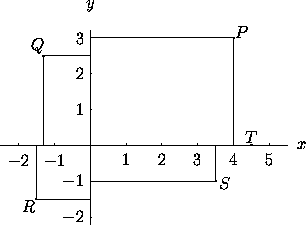
Figure 1:
In cartesian coordinates, P=(4,3),
Q=(-1.3,2.5), R=(-1.5,-1.5), S=(3.5,-1), and
T=(4.5,0). The axes divide the plane into four quadrants:
P is in the first quadrant, Q in the second, R in the
third, and S in the fourth.
T is on the positive x-axis.
Next: 1.3 Polar Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1.1 Substitutions and Transformations
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page