Next: 1.4 Homogeneous Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1.2 Cartesian Coordinates in the Plane
In polar coordinates a point P is also characterized by two
numbers: the distance r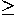 0 to a fixed pole or origin O,
and the angle
0 to a fixed pole or origin O,
and the angle  the ray OP makes with a fixed ray originating at
O, which is generally drawn pointing to the right (this is called
the initial ray). The angle
the ray OP makes with a fixed ray originating at
O, which is generally drawn pointing to the right (this is called
the initial ray). The angle
 is only defined up to a multiple of 360° or 2
is only defined up to a multiple of 360° or 2 .
In addition, it is sometimes convenient to relax the condition r
.
In addition, it is sometimes convenient to relax the condition r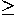 0
and allow r to be a signed distance, so (r,
0
and allow r to be a signed distance, so (r, ) and
(-r,
) and
(-r,  +180°) represent the same point
(Figure 1).
+180°) represent the same point
(Figure 1).
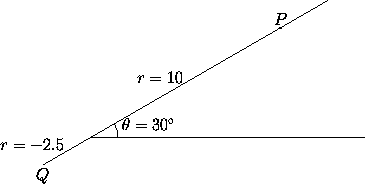
Figure 1: Among the possible sets of polar coordinates for P are:
(10, 30°),
(10, 390°)
and (10, -330°).
Among the sets of polar coordinates for Q are:
(2.5, 210°)
and (-2.5, 30°).
Consider a system of polar coordinates and a system of cartesian
coordinates with the same origin. Assume the initial ray of the polar
coordinate system coincides with the positive x-axis, and that the
ray  =90° coincides with the positive y-axis. Then
the polar coordinates (r,
=90° coincides with the positive y-axis. Then
the polar coordinates (r, ) and the cartesian coordinates
(x,y) of the same point are related as follows:
) and the cartesian coordinates
(x,y) of the same point are related as follows:
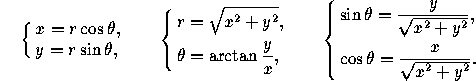
Next: 1.4 Homogeneous Coordinates in the Plane
Up: 1 Coordinate Systems in the Plane
Previous: 1.2 Cartesian Coordinates in the Plane
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.
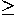 0 to a fixed pole or origin O,
and the angle
0 to a fixed pole or origin O,
and the angle  the ray OP makes with a fixed ray originating at
O, which is generally drawn pointing to the right (this is called
the initial ray). The angle
the ray OP makes with a fixed ray originating at
O, which is generally drawn pointing to the right (this is called
the initial ray). The angle
 is only defined up to a multiple of 360° or 2
is only defined up to a multiple of 360° or 2 .
In addition, it is sometimes convenient to relax the condition r
.
In addition, it is sometimes convenient to relax the condition r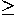 0
and allow r to be a signed distance, so (r,
0
and allow r to be a signed distance, so (r, ) and
(-r,
) and
(-r,  +180°) represent the same point
(Figure 1).
+180°) represent the same point
(Figure 1).

![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page