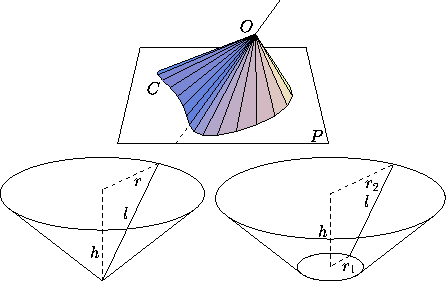
Figure 1: Top: a cone with vertex O and directrix C. Bottom left: a right circular cone. Bottom right: A frustum of the latter.
Next: 14 Spheres
Up: 13 Polyhedra
Previous: 13.2 Cylinders
Given a curve C in a plane P and a point O not in P, the cone with vertex O and directrix C is the surface obtained as the union of all lines that join O with points of C. If O is the origin and the surface is given implicity by an algebraic equation, that equation is homogeneous (all terms have the same total degree in the variables). Conversely, any homogeneous implicit equation (or one that can be made homogeneous by a change of coordinates) represents a cone.
If C is a simple closed curve, we also apply the word cone to the solid enclosed by the surface generated in this way (Figure 1, top).

Figure 1: Top: a cone with vertex O and directrix
C. Bottom left: a right circular cone.
Bottom right: A frustum of the latter.
The volume contained between P and the vertex O is
where A is the area in the plane P enclosed by C and h is the from O and P (measured perpendicularly).
The solid contained between P and a plane P' parallel to P (on the same side of the vertex) is called a frustum. Its volume is
where A and A' are the areas enclosed by the sections of the cone by P and P' (often called the bases of the frustum).
The most important particular case of a cone is the right circular cone (often simply called a cone). If r is the radius of the base, h is the altitude, and l is the length between the vertex and a point on the base circle (Figure 1, bottom left), we have the following relations:
| l |
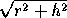 |
| lateral area |
 rl= rl= r r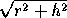 |
| total area |
 r(l+r)= r(l+r)= r(r+ r(r+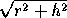 ) ) |
| volume |
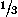  r r h h
|
The implicit equation of this surface can be written
x +y
+y =z
=z ;
;
see also Section 16.
For a frustum of right circular cone (Figure 1, bottom right) we have:
| l |
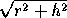 , where r=r , where r=r -r -r |
| lateral area |
 (r (r +r +r )l )l
|
| total area |
 (r (r  +r +r  +(r +(r +r +r )l) )l)
|
| volume |
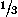  h(r h(r  +r +r  +r +r r r ) ) |
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.