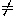 0):
0):
Up: Part II: Three-Dimensional Geometry
Previous: 15 Surfaces of Revolution. The Torus
A surface defined by an algebraic equation of degree two is called a
quadric. Spheres, circular cylinders, and circular cones are
quadrics. By means of a rigid motion, any quadric can be transformed
into a quadric having one of the following equations (where a,b,c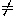 0):
0):
| (1) | Real ellipsoid | x /a /a +y +y /b /b +z +z /c /c =1 =1 |
| (2) | Imaginary ellipsoid | x /a /a +y +y /b /b +z +z /c /c =-1 =-1 |
| (3) | Hyperboloid of one sheet | x /a /a +y +y /b /b -z -z /c /c =1 =1 |
| (4) | Hyperboloid of two sheets | x /a /a +y +y /b /b -z -z /c /c =-1 =-1 |
| (5) | Real quadric cone | x /a /a +y +y /b /b -z -z /c /c =0 =0 |
| (6) | Imaginary quadric cone | x /a /a +y +y /b /b +z +z /c /c =0 =0 |
| (7) | Elliptic paraboloid | x /a /a +y +y /b /b +2z=0 +2z=0 |
| (8) | Hyperbolic paraboloid | x /a /a -y -y /b /b +2z=0 +2z=0 |
| (9) | Real elliptic cylinder | x /a /a +y +y /b /b =1 =1 |
| (10) | Imaginary elliptic cylinder | x /a /a +y +y /b /b =-1 =-1 |
| (11) | Hyperbolic cylinder | x /a /a -y -y /b /b =1 =1 |
| (12) | Real intersecting planes | x /a /a -y -y /b /b =0 =0 |
| (13) | Imaginary intersecting planes | x /a /a +y +y /b /b =0 =0 |
| (14) | Parabolic cylinder |
x +2y=0 +2y=0 |
| (15) | Real parallel planes |
x =1 =1 |
| (16) | Imaginary parallel planes |
x =-1 =-1 |
| (17) | Coincident planes |
x =0 =0 |
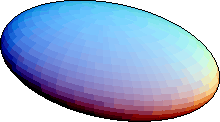
Figure 1: The ellipsoid
(1).
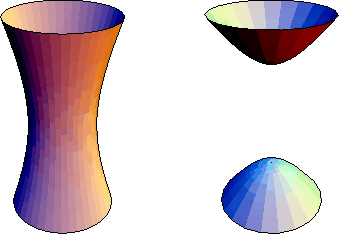
Figure 2: Left: hyperboloid of one sheet
(3).
Right: hyperboloid of two sheets
(4).
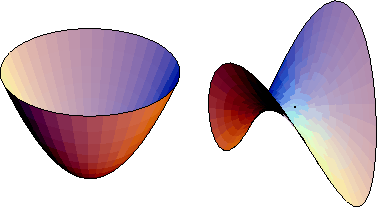
Figure 3: Left: elliptic paraboloid
(7).
Right: hyperbolic paraboloid
(8).
Surfaces with equations (9) --(17) are cylinders over the planes curves of the same equation (Section 13.2). Equations (2), (6), (10), (16), have no real solutions, so they do not describe surfaces in real three-dimensional space. A surface with equation (5) can be regarded as a cone (Section 13.3) over a conic C (any ellipse, parabola or hyperbola can be taken as the directrix; there is a two-parameter family of essentially distinct cones over it, determined by the position of the vertex with respect to C). The real nondegenerate quadrics (1), (3), (4), (7), and (8) are shown in Figures 1--3.
The surfaces with equations (1) --(6) are central quadrics; in the form given, the center is at the origin. The quantities a, b, c are the semiaxes.
The volume of the ellipsoid with semiaxes a, b, c is
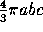 . When two of the semiaxes are the same, we can
also write the area of the ellipsoid in closed form. Suppose
b=c, so the ellipsoid x
. When two of the semiaxes are the same, we can
also write the area of the ellipsoid in closed form. Suppose
b=c, so the ellipsoid x /a
/a +(y
+(y +z
+z )/b
)/b =1 is the surface of
revolution obtained by rotating the ellipse x
=1 is the surface of
revolution obtained by rotating the ellipse x /a
/a +y
+y /b
/b =1 around
the x-axis. Its area is
=1 around
the x-axis. Its area is
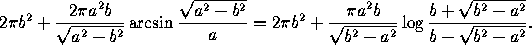
The two quantities are equal, but only one avoids complex numbers, depending on whether a>b or a<b. When a>b, we have a prolate spheroid, that is, an ellipse rotated around its major axis; when a<b we have an oblate spheroid, which is an ellipse rotated around its minor axis.
Given a general quadratic equation in three variables,
ax +by
+by +cz
+cz +2fyz+2gzx+2hxy+2px+2qy+2rz+d=0,
+2fyz+2gzx+2hxy+2px+2qy+2rz+d=0,
one can find out the type of conic it determines by consulting the following table:
 |
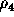 |
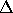 |
k signs | K signs | Type of quadric |
| 3 | 4 | <0 | real ellipsoid | ||
| 3 | 4 | >0 | same | imaginary ellipsoid | |
| 3 | 4 | >0 | opposite | hyperboloid of one sheet | |
| 3 | 4 | <0 | opposite | hyperboloid of two sheets | |
| 3 | 3 | opposite | real quadric cone | ||
| 3 | 3 | same | imaginary quadric cone | ||
| 2 | 4 | <0 | same | elliptic paraboloid | |
| 2 | 4 | >0 | opposite | hyperbolic paraboloid | |
| 2 | 3 | same | opposite | real elliptic cylinder | |
| 2 | 3 | same | same | imaginary elliptic cylinder | |
| 2 | 3 | opposite | hyperbolic cylinder | ||
| 2 | 2 | opposite | real intersecting planes | ||
| 2 | 2 | same | imaginary intersecting planes | ||
| 1 | 3 | parabolic cylinder | |||
| 1 | 2 | opposite | real parallel planes | ||
| 1 | 2 | same | imaginary parallel planes | ||
| 1 | 1 | coincident planes |
The columns have the following meaning. Let
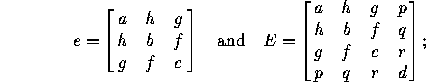
let 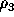 and
and 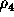 be the ranks of e and E, and let
be the ranks of e and E, and let
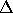 be the determinant of E. The column ``k signs'' refers
to the nonzero eigenvalues of e, that is, the roots of
be the determinant of E. The column ``k signs'' refers
to the nonzero eigenvalues of e, that is, the roots of
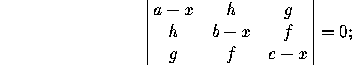
if all nonzero eigenvalues have the same sign, choose ``same'', otherwise ``opposite''. Similarly, ``K signs'' refers to the sign of the nonzero eigenvalues of E.
Up: Part II: Three-Dimensional Geometry
Previous: 15 Surfaces of Revolution. The Torus
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.