 ,y
,y ,z
,z ) has equation
) has equation
Next: 15 Surfaces of Revolution. The Torus
Up: Part II: Three-Dimensional Geometry
Previous: 13.3 Cones
The set of points in space whose distance to a fixed point (the center) is
a fixed positive number (the radius) is a sphere.
A circle of radius r and center (x ,y
,y ,z
,z ) has equation
) has equation
(x-x )
) +(y-y
+(y-y )
) +(z-z
+(z-z )
) =r
=r ,
,
or
x +y
+y +z
+z -2xx
-2xx -2yy
-2yy -2zz
-2zz +x
+x
 +y
+y
 +z
+z
 -r
-r =0.
=0.
Conversely, an equation of the form
x +y
+y +z
+z +2dx+2ey+2fz+g=0
+2dx+2ey+2fz+g=0
defines a sphere if d +e
+e +f
+f >g; the center is
(-d, -e, -f)
and the radius is
>g; the center is
(-d, -e, -f)
and the radius is 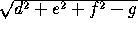 .
.
Four points not on the same plane determine a unique sphere.
If the points have coordinates (x ,y
,y ,z
,z ),
(x
),
(x ,y
,y ,z
,z ), (x
), (x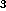 ,y
,y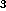 ,z
,z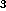 ) and (x
) and (x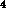 ,x
,x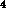 ,z
,z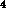 ), the equation
of the sphere is
), the equation
of the sphere is
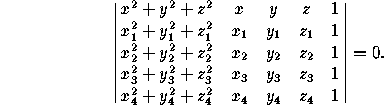
Given two points P =(x
=(x ,y
,y ,z
,z ) and
P
) and
P =(x
=(x ,y
,y ,z
,z ),
there is a unique sphere whose diameter is P
),
there is a unique sphere whose diameter is P P
P ;
its equation is
;
its equation is
(x-x )(x-x
)(x-x )+(y-y
)+(y-y )(y-y
)(y-y )+(z-z
)+(z-z )(z-z
)(z-z )=0.
)=0.
The area of a sphere of radius r is
4 r
r , and the volume is
, and the volume is 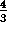
 r
r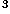 .
.
The area of a spherical polygon (that is, of a polygon on the sphere whose sides are arcs of great circles) is
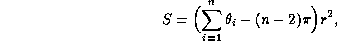
where r is the radius of the sphere, n is the number of vertices,
and the 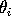 are the internal angles of the polygons in radians.
In particular, the sum of the angles of a spherical triangle is always
greater than
are the internal angles of the polygons in radians.
In particular, the sum of the angles of a spherical triangle is always
greater than  =180°, and the excess is proportional to the
area.
=180°, and the excess is proportional to the
area.
Let the radius be r (Figure 1, left).
The area of the curved region is 2 rh=
rh= p
p . The
volume of the cap is
. The
volume of the cap is 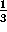
 h
h (3r-h)=
(3r-h)=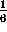
 h(3a
h(3a +h
+h ).
).
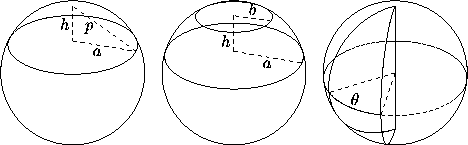
Figure 1: Left: a spherical cap. Middle: a spherical zone (of two
bases). Right: a spherical segment.
Let the radius be r (Figure 1, middle).
The area of the curved region is 2 rh. The
volume of the zone is
rh. The
volume of the zone is 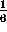
 h(3a
h(3a +3b
+3b +h
+h ).
).
Let the radius be r (Figure 1, right). The area of
the curved region (lune) is 2r
 , the angle being measured in
radians. The volume of the segment is
, the angle being measured in
radians. The volume of the segment is 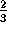 r
r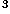
 .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.