 ,y
,y ) has equation
) has equation
Next: 7 Conics
Up: Part I: Two-Dimensional Geometry
Previous: 5.3 Regular Polygons
The set of points whose distance to a fixed point (the center) is
a fixed positive number (the radius) is a circle.
A circle of radius r and center (x ,y
,y ) has equation
) has equation
(x-x )
) +(y-y
+(y-y )
) =r
=r ,
,
or
x +y
+y -2xx
-2xx -2yy
-2yy +x
+x
 +y
+y
 -r
-r =0.
=0.
Conversely, an equation of the form
x +y
+y +2dx+2ey+f=0
+2dx+2ey+f=0
defines a circle if d +e
+e >f; the center is (-d, -e)
and the radius is
>f; the center is (-d, -e)
and the radius is 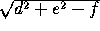 .
.
Three points not on the same line determine a unique circle.
If the points have coordinates (x ,y
,y ),
(x
),
(x ,y
,y ) and (x
) and (x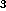 ,y
,y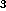 ), the equation
of the circle is
), the equation
of the circle is
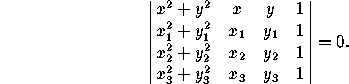
A chord of a circle is a line segment between two points
(Figure 1). A diameter is a chord that goes through
the center, or the length of such a chord (therefore the diameter is
twice the radius). Given two points P =(x
=(x ,y
,y ) and
P
) and
P =(x
=(x ,y
,y ), there is a unique circle whose diameter is
P
), there is a unique circle whose diameter is
P P
P ;
its equation is
;
its equation is
(x-x )(x-x
)(x-x )+(y-y
)+(y-y )(y-y
)(y-y )=0.
)=0.
The length or circumference of a circle of radius r is
2 r, and the area is
r, and the area is  r
r . The length of the arc
of circle subtended by an angle
. The length of the arc
of circle subtended by an angle  , shown as s in
Figure 1, is r
, shown as s in
Figure 1, is r . Other relations between the
radius, the arc length, the chord, and the areas of the corresponding
sector and segment are, in the notation of
(Figure 1):
. Other relations between the
radius, the arc length, the chord, and the areas of the corresponding
sector and segment are, in the notation of
(Figure 1):
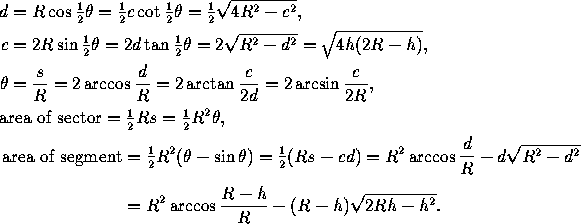
Figure 1: The arc of circle subtendend by the angle  is s;
the chord is c; the sector is the whole slice of the pie; the
segment is the cap bounded by the arc and the chord (that is, the
slice minus the triangle).
is s;
the chord is c; the sector is the whole slice of the pie; the
segment is the cap bounded by the arc and the chord (that is, the
slice minus the triangle).
Other properties of circles:
 , the angle ACB, where C
is any point on the circle, equals ½
, the angle ACB, where C
is any point on the circle, equals ½ or
180°-½
or
180°-½ (Figure 2, left).
Conversely, given a segment AB, the set of points that ``sees'' AB
under a fixed angle is an arc of a circle (Figure 2,
right). In particular, the set of points that see AB under a right
angle is a circle with diameter AB.
(Figure 2, left).
Conversely, given a segment AB, the set of points that ``sees'' AB
under a fixed angle is an arc of a circle (Figure 2,
right). In particular, the set of points that see AB under a right
angle is a circle with diameter AB.
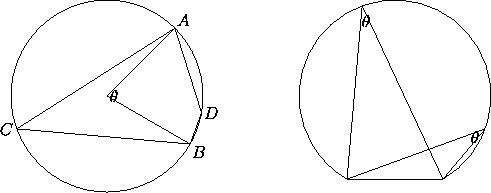
Figure 2: Left: The angle ACB equals ½ for any C in
the long arc AB; and ADB equals 180°-½
for any C in
the long arc AB; and ADB equals 180°-½ for any D in
the short arc AB. Right: The locus of points from which the segment
AB subtends a fixed angle
for any D in
the short arc AB. Right: The locus of points from which the segment
AB subtends a fixed angle  is an arc of circle.
is an arc of circle.
 , P
, P , P
, P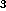 , P
, P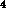 be points in the plane, and let
be points in the plane, and let
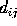 , for 1
, for 1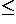 i,j
i,j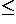 4, be the distance between
4, be the distance between 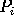 and
and
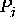 . A necessary and sufficient condition for the points to all lie
on the same circle (or line) is that one of the following equalities
be satisfied:
. A necessary and sufficient condition for the points to all lie
on the same circle (or line) is that one of the following equalities
be satisfied:
±d
 d
d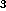
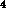 ±d
±d
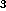 d
d
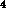 ±d
±d
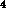 d
d
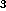 =0.
=0.
This is equivalent to Ptolemy's formula for cyclic quadrilaterals
![]() .
.
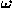 , a circle of
center (x
, a circle of
center (x ,y
,y ) and radius r has equation
) and radius r has equation
(x-x )
) + (y-y
+ (y-y )
) +
2(x-x
+
2(x-x )(y-y
)(y-y ) cos
) cos 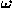 =r
=r .
.
A circle of radius a, passing through the pole,
and with center at the point (r, )=(a,
)=(a,
 ) has
equation
) has
equation
r=2a cos( -
-
 ).
).
A circle of radius a and with center at the point
(r, )=(r
)=(r ,
,
 ) has equation
) has equation
r -2r
-2r r cos(
r cos( -
-
 )+r
)+r
 -a
-a =0.
=0.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.