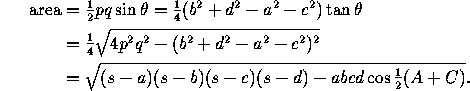
Next: 5.3 Regular Polygons
Up: 5 Polygons
Previous: 5.1 Triangles
The following formulas give the area of a general quadrilateral (see Figure 1, left, for the notation).
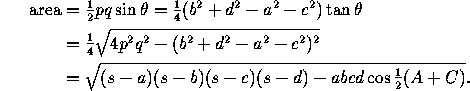
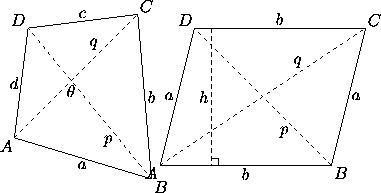
Figure 1: Left: notation for a general quadrilateral; in addition
s=½(a+b+c+d). Right: a parallelogram.
Often, however, it is easiest to compute the area by dividing the quadrilateral into triangles. One can also divide into triangles to compute one side given the other sides and angles, etc.
More formulas can be given for special cases of quadrilaterals. In a parallelogram opposite sides are parallel (Figure 1, right). It follows that opposite sides have the same length and that two consecutive angles add up to 180°. In the notation of the figure, we have
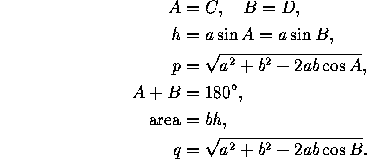
(All this follows from the triangle formulas applied to the triangles ABD and ABC.)
Two particular cases of parallelograms are:
 , where all angles equal 90°. The diagonals
of a rectangle have the same length. The general formulas for
parallelograms reduce to
, where all angles equal 90°. The diagonals
of a rectangle have the same length. The general formulas for
parallelograms reduce to
h=a
area=ab
p=q=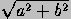 .
.
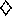 , where adjacent sides
have the same length (a=b). The diagonals of a rhombus are
perpendicular. In addition to the general
formulas for parallelograms we have area=½pq and
p
, where adjacent sides
have the same length (a=b). The diagonals of a rhombus are
perpendicular. In addition to the general
formulas for parallelograms we have area=½pq and
p +q
+q =4a
=4a .
.
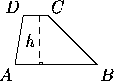
A quadrilateral is a trapezoid if two sides are parallel. In the notation of the figure below we have
A+D=B+C=180°,
area=½(AB+CD)h.
A quadrilateral is cyclic if it can be inscribed in a circle, that is, if its four vertices belong to a single, circumscribed, circle. This is possible if and only if the sum of opposite angles is 180°. If R is the radius of the circumscribed circle, we have (in the notation of Figure 1, left):
A quadrilateral is circumscribable if it has an inscribed circle (that is, a circle tangent to all four sides). Its area is rs, where r is the radius of the inscribed circle and s is as above.
For a quadrilateral that is both cyclic and circumscribable we have the following additional equalities, where m is the distance between the centers of the inscribed and circumscribed circles:
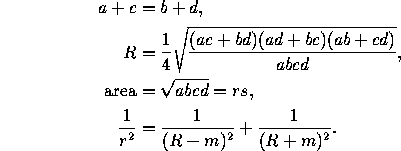
Additional fact about quadrilaterals:
 +c
+c =b
=b +d
+d .
.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.