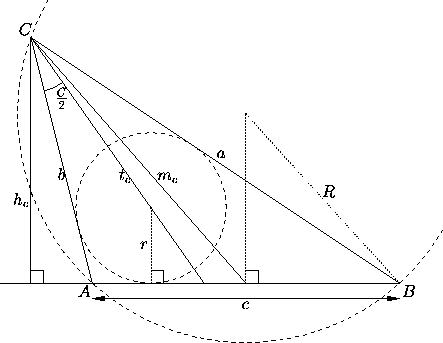
Figure 1: Notations for an arbitrary triangle of sides a, b, c and vertices A, B, C. The altitude corresponding to C is
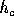 , the median is
, the median is 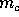 , the bisector is
, the bisector is 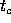 . The radius of the
circumscribed circle is R, that of the inscribed circle is r.
. The radius of the
circumscribed circle is R, that of the inscribed circle is r.
Next: 5.2 Quadrilaterals
Up: 5 Polygons
Previous: 5 Polygons
Because the angles of a triangle add up to 180°, at least two of them must be acute (less than 90°). In an acute triangle all angles are acute. A right triangle has one right angle, and an obtuse triangle has one obtuse angle.
The altitude corresponding to a side is the perpendicular dropped to the line containing that side from the opposite vertex. The bisector of a vertex is the line that divides the angle at that vertex into two equal parts. The median is the segment joining a vertex to the midpoint of the opposite side. See Figure 1.

Figure 1: Notations for an arbitrary triangle of sides a, b, c
and vertices A, B, C. The altitude corresponding to C is
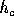 , the median is
, the median is 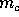 , the bisector is
, the bisector is 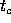 . The radius of the
circumscribed circle is R, that of the inscribed circle is r.
. The radius of the
circumscribed circle is R, that of the inscribed circle is r.
Every triangle also has an inscribed circle tangent to its sides and interior to the triangle (in other words, any three nonconcurrent lines determine a circle). The center of this circle is the point of intersection of the bisectors. We denote the radius of the inscribed circle by r.
Every triangle has a circumscribed circle going through its vertices; in other words, any three noncollinear points determine a circle. The point of intersection of the medians is the center of mass of the triangle (considered as an area in the plane). We denote the radius of the circumscribed circle by R.
Introduce the following notations for an arbitrary triangle of
vertices A, B, C and sides a, b, c (see
Figure 1). Let 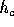 ,
, 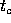 and
and 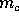 be the lengths
of the altitude, bisector and median originating in vertex C, let
r and R be as usual the radii of the inscribed and circumscribed
circles, and let s=½(a+b+c). Then:
be the lengths
of the altitude, bisector and median originating in vertex C, let
r and R be as usual the radii of the inscribed and circumscribed
circles, and let s=½(a+b+c). Then:
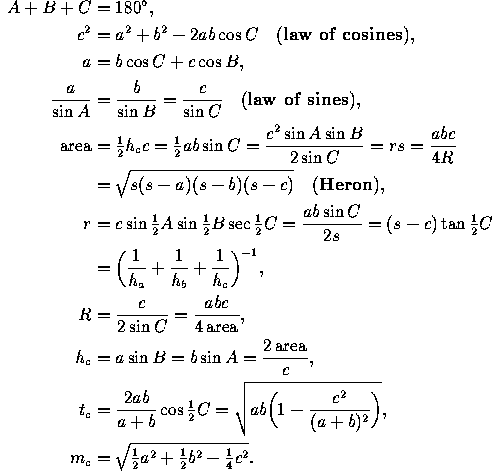
A triangle is equilateral if all its sides have the same length, or, equivalently, if all its angles are the same (and equal to 60°). It is isosceles if two sides are the same, or, equivalently, if two angles are the same. Otherwise it is scalene.
For an equilateral triangle of side a we have:
area=¼a
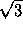 ,
,
r=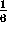 a
a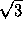 ,
,
R=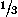 a
a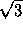 ,
,
h=½a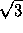 ,
,
where h is any altitude. The altitude, the bisector and the median for each vertex coincide.
For an isosceles triangle, the altitude for the unequal side is also the corresponding bisector and median, but this is not true for the other two altitudes. Many formulas for an isosceles triangle of sides a, a, c can be immediately derived from those for a right triangle of legs a, ½c (see Figure 2, left).
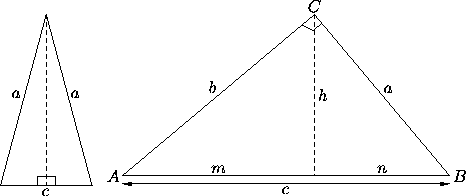
Figure 2: Left: An isosceles triangle can be divided into two congruent
right triangles. Right: notations for a right triangle.
For a right triangle the hypothenuse is the longest side opposite the right angle; the legs are the two shorter sides, adjacent to the right angle. The altitude for each leg equals the other leg. In Figure 2 (right), h denotes the altitude for the hypothenuse, while m and n denote the segments into which this altitude divides the hypothenuse.
The following formulas apply for a right triangle:
A+B=90°
r=ab/(a+b+c)
a=c sin A = c cos B
mc=b
area=½ab
c =a
=a +b
+b (Pythagoras)
(Pythagoras)
R=½c
b=c sin B = c cos A
nc=a
hc=ab
The hypothenuse is a diameter of the circumscribed circle. The median joining the midpoint of the hypothenuse (the center of the circumscribed circle) to the right angle makes angles 2A and 2B with the hypothenuse.
Additional facts about triangles:
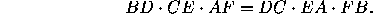
This is so in three important particular cases: when the three lines are the medians, when they are the bisectors, and when they are the altitudes.
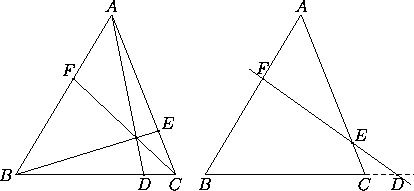
Figure 3: Left: Ceva's Theorem. Right: Menelaus's Theorem.
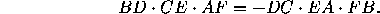
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home PageSilvio Levy
Wed Oct 4 16:41:25 PDT 1995
This document is excerpted from the 30th Edition of the CRC Standard Mathematical Tables and Formulas (CRC Press). Unauthorized duplication is forbidden.