The Nephroid Lab
Welcome to The Nephroid Lab, an interactive laboratory in
elementary computational algebraic geometry.
The immediate goal of this lab is to
show that two curves defined by the pictures below are the same.
Both are called the nephroid, because of their kidney shape.

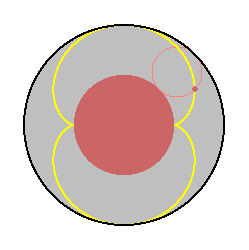
Figure 1: An optical and mathematical nephroid curve.
The apparent curve in the first image is the pattern formed on the bottom of
an empty flat-bottomed coffee mug when parallel light rays
come in and bounce off the circular sides.
The similar looking curve in the second image is the path
traced out by a point on the boundary of a small disk as the
disk rolls along the boundary of a larger disk having twice
the diameter.
In figuring out why the two nephroid curves are the same, we will
encounter the following mathematical ideas:
- How to find a parametrization in terms of trigonometric functions
for curves (like the nephroid) that may be generated by rolling
one circle along the outside of another circle.
- How to convert trigonometric parametrizations into
algebraic parametrizations.
- How to use elimination of variables to
- find implicit polynomial equations for parametrized curves
- compute profiles of projections of algebraic surfaces,
profiles of surfaces, and envelopes of families of curves
Lab Outline
Other Topics
References and sources of inspiration
The following sources provided many of the ideas for this lab.
One might also consult them for more precise formulations
of the concepts it attempts to teach.
We also include here a link to some text describing the
intended audience and usage for the lab.
Next: Parametrizing the Nephroid
The authors would like to thank Stuart Levy for helping to photograph
the coffee cup nephroid on this title page.
Vic Reiner <reiner@math.umn.edu>
Frederick J. Wicklin <fjw@geom.umn.edu>
URL for this page: http://www.geom.umn.edu/~fjw/calc-init/nephroid/
Last modified: Thu May 2 10:41:12 1996



