Conclusions
The computation of the envelope showed that indeed, the
nephroid curve is part of the envelope of the family of
reflected light rays, which explains how it ended up on
the bottom of your coffee cup. But it also raises some
questions:
- Why are there extra factors x2 y2 present in
the envelope? What curves are defined by the equations
x2 = 0 and y2 = 0, and why should these curves
be part of the envelope?
- Why do these curves appear "doubled", i.e. why is
it x2 = 0 and y2 = 0 rather than just x=0 and y=0?
The first two questions start to make sense when we look closely
at the graph surface F(t,x,y)=0 shown below, and think about
how its singularities relate to the envelope. You can click on the
picture to generate an MPEG movie (646 Kbytes).
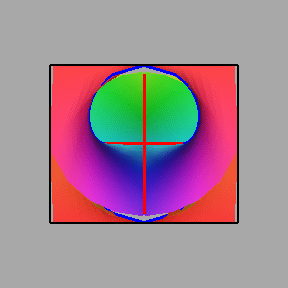
If you haven't read about
projections, profiles, and envelopes,
take a look at it now. Given an algebraic surface like
F(t,x,y)=0, there is also a notion of its
singular set which you can also read about.
Question 8
- After reading about singular sets and profiles and envelopes,
explain why the following statement is true: For any surface F(t,x,y)=0,
the projection of its singular set onto the xy-plane will always show
up as a subset of the t-profile of the surface.
- Go back to the page about singular sets and look at the Maple
computation of singularities on our graph surface.
Which of the curves in the singular set project down to
the "extra" pieces of the envelope x2=0 and y2=0?
- Does the picture of the singular set inside the surface give you any
clue as to why these curves appear "doubled",
i.e. x2=0 and y2=0 rather than x=0 and y=0?
Previous:
Computing the Envelope of a Family of Curves
Up: Introduction
Vic Reiner <reiner@math.umn.edu>
Frederick J. Wicklin <fjw@geom.umn.edu>
Last modified: Mon Apr 15 13:53:47 1996
