Projections, Profiles, and Envelopes
"Elimination = Projection"
Suppose we are given a system of equations, for example
y-x2=0
z-x3=0
that defines a curve in (x,y,z) 3-space
called the twisted cubic curve, whose projection onto
the yz-plane is shown below. You can click on the graph of the projection
to generate an MPEG movie (308K) of the curve in 3-space.
If we try to eliminate the variable x from those
equations, we can produce the equation z2-y3=0, which is
the curve with a cusp in the yz-plane:
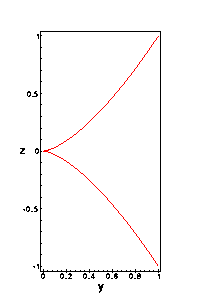
The curve z2 - y3=0.
If you project the twisted cubic curve orthogonally onto the
yz-plane, this curve with a cusp is exactly what you hit.
It should at least be clear that the equation z2-y3 produced
by elimination of the variable x is satisfied by all points
in the projection, since the projection map takes a point
(x,y,z) satisfying the first two equations (and hence also
satisfying z2-y3) and maps it to (y,z).
Questions to think about
What equation will describe the projection of the
twisted cubic onto the xy-plane? What about onto the
xz-plane?
More generally, if we are given a system of equations
f1(x1,...,xn)=0
f2(x1,...,xn)=0
etc.
they define a subset V of the n-space with coordinates
x1,..., xn,
Then any equations g(xk,xk+1,...,xn)=0 obtained
from the fi's by elimination of the variables
x1,...,xk-1
will be satisfied by all points in the projection of V onto
the (n-k+1)-subspace with coordinates xk,xk+1,...,xn.
This is part of what we mean by "elimination = projection".
For a more detailed discussion of the case where the fi
are polynomials, and a more precise statement about the relation
between elimination and projection in this case, see
Cox, Little, and O'Shea Sections 3.1 and 3.2.
Profiles of Surfaces
Suppose we are looking at a surface S in 3-space with coordinates
(x,y,z), and our viewpoint is from above on the z-axis. For
example, take the tilted torus shown below.
If we were to draw a 2-dimensional line drawing of the
torus projected onto the xy-plane, certain points of the torus will
show up in this silhouette (or shadow or profile)
while others will not:

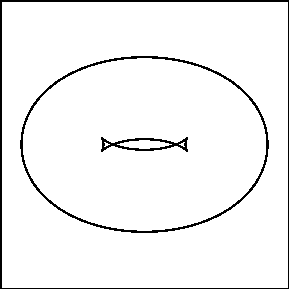
The tilted torus and its shadow on the xy-plane
How did we decide which points (x,y,z) on the torus to project into
the plane? If you stare at the picture and think about it,
you'll see that we chose to project the points where the tangent plane to the
torus is parallel to the z-axis. We will call this set the
z-profile of the surface.
To find equations in x,y that contain the z-profile, we must eliminate
the variable z from the equations in x,y,z that define points on the
torus that have tangent plane parallel to the z-axis. So first
we need to figure out what those equations are.
Questions to think about
- Explain how to calculate the normal vector at a point P on the surface
f(x,y,z)=0 using facts about tangent planes and normals to level sets
of a function that you learned in multivariable calculus.
(Hint: the gradient vector (df/dx, df/dy, df/dz) of f evaluated
at P is involved somehow).
- Once you have the normal vector at P, how can you describe the condition
that the tangent plane is parallel to the z-axis?
- Put this together to explain why the points in the z-profile should
be the projections to the xy-plane of the solutions (x,y,z) of
f(x,y,z)=0
d/dz f(x,y,z)=0
This suggests that if f(x,y,z) is a polynomial, we could compute
the equation for the z-profile of the surface f(x,y,z)=0
using a Gröbner basis computation in Maple to eliminate
variables from the two equations above. This is exactly what we
did for the tilted torus.
Envelope of a Family of Curves
If we are given a family of curves Ct defined by F(t,x,y)=0 in the
xy-plane, a curve which has a common tangent with each one of curves Ct is
said to be part of the envelope of Ct. For example, if
Ct is the family of circles of radius t3/3
centered about the point (t2,t3/3)
for various values of t, pictured below, with part of its envelope
highlighted:
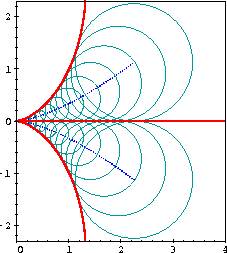
The family of circles and its envelope curves
Questions to think about
What is the equation F(t,x,y) = 0 defining Ct in this case?
Try to write down a polynomial equation, i.e. one that avoids
square roots.
We would like to be able to compute an equation satisfied by
the points of the envelope if we are given the equation F(t,x,y)=0.
The key observation is this: the envelope is a subset of the
t-profile of the surface defined by F(t,x,y)=0 in (t,x,y)-space,
as shown below. Click on the graphic to generate an MPEG movie
(410 Kbytes) of this surface.
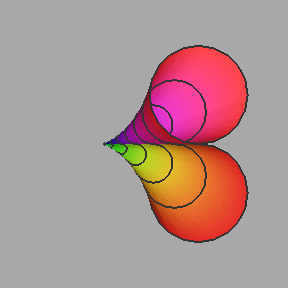
The surface F(t,x,y)=0 produced by the family of circles
This then suggests that when F(t,x,y) is a polynomial,
we can follow the recipe for computing the t-profile of the
surface F(t,x,y) to find the equations satisfied by the
points of the envelope. That is, we eliminate t (using a Gröbner
basis computation) from the equations
F(t,x,y)=0
d/dt F(t,x,y)=0
Here is the computation for the family of circles we discussed earlier:
>F:=(x-t^2)^2+(y-t^3/3)^2-(t^3/3)^2;
2 2 3 2 6
F := (x - t ) + (y - 1/3 t ) - 1/9 t
> GB:=gbasis({F,diff(F,t)},[t,x,y],plex);
Only the 7th (last) polynomial in the resulting Gröbner
basis did not involve t, so by factoring it we obtain
the equations for the envelope curves:
> factor(GB[7]);
2 2 3 2 2 2 2 4
y (x + y ) (64 x + 3 y x + 72 y x - 144 y + 3 y )
The resulting implicit equation for the envelope can then be plotted to
obtain the red curves in the 4th figure on this page.
Questions to think about
- Can you explain why the ``extra" factor y shows up in the envelope
equation? What does it correspond to in the picture of the envelope?
- Does the extra factor x2+y2 in the envelope
equation correspond to something you can see in the picture?
For a different (and more detailed) discussion of envelopes, see
Cox, Little, and O'Shea Section 3.4. For an even deeper discussion,
see Bruce and Giblin.
Go To:
Computing the Envelope of a Family of Curves
Go To:
Gröbner bases and Elimination of Variables
Up: Introduction
Vic Reiner <reiner@math.umn.edu>
Frederick J. Wicklin <fjw@geom.umn.edu>
Last modified: Thu Apr 25 08:20:55 1996



