The Geometry of Reflecting Light Rays
When parallel rays of light enter the coffee cup at an oblique
angle, they bounce off the circular side of the cup at various angles,
and then hit the bottom of the cup and form the pattern
shown on the introductory page. Such patterns formed by reflecting
light rays bouncing off objects are called caustics.
We can model this situation by letting
the side of the coffee cup be the semicircle of radius 2 shown below,
and imagining the parallel light rays coming in horizontal along
the lines y=t for various values of t, and reflecting outward.
Group Activity
Simulate this physical process to see how
light rays bounce off the semicircle as
the value of t varies.
Physics tells us that when the light ray hits the semicircle,
we can compute the angle it will bounce off as follows: draw
the normal N to the tangent line T at the point of impact, and
the angle of incidence a between the incoming ray and N will
be the same as the angle of reflection b between the outgoing ray
and N. See the following diagram:
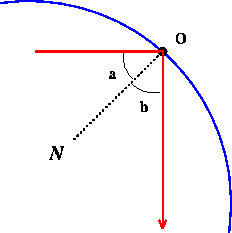
Figure 4: The angle of incidence, a is equal to the angle of
reflection, b.
Question 4
- If the origin is at the center of the semicircle,
what are the (x,y) coordinates for the point on the
semicircle of radius 2 that the light ray at y=t hits?
- What is the slope of the normal N to the tangent T of
the semicircle at that point?
- Can you use the above information to deduce a formula for
tan(a) in terms of t, where a is the angle of
incidence between the light ray at y=t and the normal N?
What about similar formulas for sin(a), cos(a)?
- Explain (first to yourself, then on paper)
why the slope of the reflected line should be tan(2a).
- By expressing tan(2a) in terms of
sin(a), cos(a),
can you come up with a formula just in terms of t for the
slope of the line reflected from y=t?
Question 5
You now have a formula in terms of t for the slope of
the reflected line and a point on that line (namely, the
point of impact). Therefore using the point-slope formula
for a line, you should be able to write down an equation in
t,x,y that defines the line reflected from the light ray at
y=t.
If you would like to compare with our answer (which may
not look exactly the same), we got the equation:
y-t = t sqrt(4-t2)/(2-t2) (x - sqrt(4-t2))
Next:
Computing the Envelope of a Family of Curves
Previous:
Transforming a Parametrization into an Implicit Algebraic Equation
Up: Introduction
Vic Reiner <reiner@math.umn.edu>
Frederick J. Wicklin <fjw@geom.umn.edu>
Last modified: Mon Apr 15 13:55:06 1996

