Parametrizing the Nephroid
Let's consider the path followed by a point on the boundary of a
disk as it rolls around the boundary of a second disk whose radius is
twice that of the first disk. (Curves formed by rolling disks
of various radii in this manner are called epicycloids.)
We will choose the particular disks of
radius 1 and 1/2 as shown below, and follow the point on the boundary
of the smaller disk labeled P in the picture.
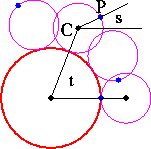
Figure 2: Following a point on a rolling circle.
To establish some notation, let's say
- R = 1 is the radius of the larger disk
- r = 1/2 is the radius of the smaller disk
- t is the angle of elevation of the center C of the smaller disk
with respect to a horizontal line going through the
center of the larger disk.
- s is the angle of elevation of P with respect to a horizontal
line going through C.
How should s and t be related in general?
Let's collect some data to figure this out.
Question 1
The Epicycloid Generator allows us to
simulate the rolling of one circle around another.
The point P that we will trace begins at 180 degrees. In other words,
when t=0, then s=180 degrees. Make a table of t
versus s values for values of t in the interval [0, 360]
and use this table to help you answer the following questions:
- How many times does s=0 as the outer circle rolls
around the inner circle? For what values of t
does this occur?
- If we stay away from the t values for which s
becomes zero, how does s change for a given change in t?
In other words, what is ds/dt?
- Use your data and the answers to the previous questions to
write down a simple formula for s as a function of t.
(Hint: even though the data indicates that the underlying function
is discontinuous, use the fact that 0 and 360 degrees represent the
same point on a circle to write down a continuous function.)
You might be surprised by the answer to the previous question,
if you had reasoned as follows: "Since the larger disk has
twice the diameter, it has twice the circumference.
Therefore the smaller disk will have
gone through twice the angular rotation as the larger one during
the same period of time, and s = 2t."
Although the above reasoning is slightly wrong, it is nevertheless
true that the small circle has half the arclength of the large circle,
and therefore as it rolls, it rotates twice due to the rolling.
If the above statement is true, then there must be another factor that
causes the small circle to rotate faster than our intuition suggests.
Question 2
Suppose the small circle does not roll around the edge of the big circle,
but rather is rigidly connected to the larger circle so that it
moves around the circle as in the figure below.
How many rotations will a dot on a non-rolling
circle make as the circle moves once around the
larger circle? Use this
write down a parametrization for the nephroid as
x = x(t), y=y(t), where
x(t), y(t) are
some trigonometric functions of t. Check that your parametrization
gives a nephroid using the
Parametric Curve Plotter.
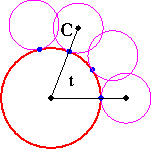
Figure 3: Following a point on a circle that rotates, but
does not roll.
Next:
Transforming a Parametrization
into an Implicit Algebraic Equation
Up:
Introduction
Vic Reiner <reiner@math.umn.edu>
Frederick J. Wicklin <fjw@geom.umn.edu>
Last modified: Thu Apr 4 14:50:09 1996


