![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
| Figure 1 | Possible dynamics on two-dimensional stable and unstable manifolds. |
| Figure 2 | The influence of the dynamics when iterating points. |
| Figure 3 | The linearized stable and unstable manifolds of a circle of saddle-type. |
| Figure 4 | The algorithm GLOBALIZE in pseudo-code. |
| Figure 5 | The procedure ADDCIRCLE in pseudo-code. |
| Figure 6 | Linear foliation near the invariant circle H. |
| Figure 7 | The map acting on triangles of 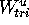 . .
|
| Figure 8 | Initial mesh near a hyperbolic fixed point. |
| Figure 9 | Mesh adaptation by adding extra leaves of the foliation. |
| Figure 10 | Two different viewpoints of the stable manifold of the 3D-fattened Arnol'd family. |
| Figure 11 | The unstable manifold of the Quasiperiodically forced Hénon map. |
| Figure 12 | Heteroclinic tangle of two-dimensional stable and unstable manifolds of the Quasiperiodically forced Hénon map. |
| Figure 13 | The unstable manifold of the origin of the example of a hyperbolic fixed point. |
| Figure 14 | Comparing the condition of the mesh when leaves are added and when not. |
| Figure 15 | The stable manifold of the Lorenz system computed by [Worfolk 1997]. |
| Figure 16 | The stable manifold of the Lorenz system computed with our algorith |
| Figure 17 | Stable and unstable manifolds of the normal form of the Hopf-Hopf bifurcation. |
| Figure 18 | A situation where the Foliation Condition is not satisfied. |
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Tue Jun 10 13:22:16 1997