![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
The 3D-fattened Arnol'd family is defined on 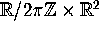 by
by
Here, 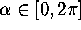 ,
, 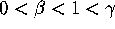 and
and
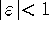 . This family is introduced
in [Osinga 1996,
Broer et al. 1996,
Broer et al. 1997] as an example of a
system with a
normally hyperbolic invariant circle of saddle-type. It is a
three-dimensional embedding of the standard
Arnol'd family of circle
maps, as can be seen by setting
. This family is introduced
in [Osinga 1996,
Broer et al. 1996,
Broer et al. 1997] as an example of a
system with a
normally hyperbolic invariant circle of saddle-type. It is a
three-dimensional embedding of the standard
Arnol'd family of circle
maps, as can be seen by setting 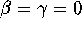 ;
see [
Arnol'd 1965]. The dynamics on the normally hyperbolic
invariant circle of (4) is
organized as for the one-dimensional family.
For
;
see [
Arnol'd 1965]. The dynamics on the normally hyperbolic
invariant circle of (4) is
organized as for the one-dimensional family.
For 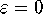 the dynamics is periodic or
quasi periodic, depending on whether
the dynamics is periodic or
quasi periodic, depending on whether 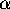 is rational or
irrational. For positive
is rational or
irrational. For positive 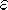 the points in parameter space where the
dynamics on the circle is phase-locked form regions, the equivalents
of the so-called
Arnol'd tongues.
the points in parameter space where the
dynamics on the circle is phase-locked form regions, the equivalents
of the so-called
Arnol'd tongues.
We study the 3D-fattened
Arnol'd map (4) for 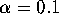 ,
, 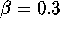 ,
, 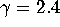 , and
, and
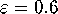 . For these
parameter values the invariant saddle-circle is still normally
hyperbolic, and it can be computed by using the adapted graph
transform of [Osinga 1996]. On the circle two saddles exist; one is
attracting and the other is repelling on the circle. The situation is
as sketched in Figure 1 (right). Let us consider
the stable manifold of the circle. The first order approximation of
this manifold is given by the data from the computations of the
invariant circle.
. For these
parameter values the invariant saddle-circle is still normally
hyperbolic, and it can be computed by using the adapted graph
transform of [Osinga 1996]. On the circle two saddles exist; one is
attracting and the other is repelling on the circle. The situation is
as sketched in Figure 1 (right). Let us consider
the stable manifold of the circle. The first order approximation of
this manifold is given by the data from the computations of the
invariant circle.
The result of our computations is shown in
Figure 10. We
computed one branch of the stable manifold, starting on the linear
approximation at distance 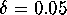 from the circle. The
invariant circle of the 3D-fattened
Arnol'd family is special in
the sense that it can always be parametrized by the x-coordinate if
the circle is normally hyperbolic. Therefore, it is natural to choose
the linear foliation
from the circle. The
invariant circle of the 3D-fattened
Arnol'd family is special in
the sense that it can always be parametrized by the x-coordinate if
the circle is normally hyperbolic. Therefore, it is natural to choose
the linear foliation 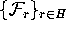 with
with 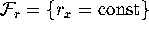 . The algorithm computes intersections with 50 of
these leaves with an accuracy of
. The algorithm computes intersections with 50 of
these leaves with an accuracy of 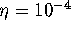 . The distance
. The distance
 between consecutive points on such intersection curves does
not exceed
between consecutive points on such intersection curves does
not exceed 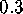 . The alternatingly colored bands on the manifold have
width
. The alternatingly colored bands on the manifold have
width 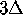 . The total length of the manifold is approximately
47; note that the length of the circle is slightly more than
. The total length of the manifold is approximately
47; note that the length of the circle is slightly more than 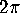 .
.
Figure 10 also shows the two (strong) stable manifolds
of the saddles on the circle. These manifolds were computed by
iterating a fundamental domain on the corresponding eigenvectors. The
first points are also at distance 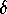 from the fixed points, and
the iteration is done with 100 points in the fundamental
domain. These curves serve as a test to show that our computations are
accurate: the two curves lie in the two-dimensional manifold; see also
Section 4. For high values of
from the fixed points, and
the iteration is done with 100 points in the fundamental
domain. These curves serve as a test to show that our computations are
accurate: the two curves lie in the two-dimensional manifold; see also
Section 4. For high values of 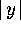 and
and
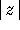 , the term
, the term 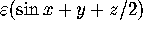 in the mapping of
the x-coordinate produces a strong rotational behavior. One extra
iteration of the one-dimensional strong stable manifolds creates seven
new windings.
in the mapping of
the x-coordinate produces a strong rotational behavior. One extra
iteration of the one-dimensional strong stable manifolds creates seven
new windings.
Note that, if one iterates a (discretized) fundamental domain on the two-dimensional manifold, points accumulate along the one-dimensional stable manifold of the saddle that is repelling on the circle (the light blue curve in Figure 10). In other words, it is hardly possible to compute the entire surface that way.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:53:51 1997