![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
The quasiperiodically forced Hénon map is defined on 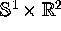 , where we identify
, where we identify 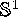 with
with 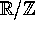 . This family is
studied in [Sosnovtseva et al. 1996], and it is defined as
. This family is
studied in [Sosnovtseva et al. 1996], and it is defined as
The rotation 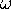 must be irrational, and in practice we choose
the golden mean
must be irrational, and in practice we choose
the golden mean 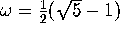 . For A = 0 we
get an uncoupling of the
. For A = 0 we
get an uncoupling of the 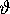 -parameter, and the system is
simply the Hénon map times a rigid rotation, so that fixed points of
the Hénon map are circles of
(5). For positive A the
structure is more complicated, and as A increases, the invariant
circles can become strange attractors; see [Sosnovtseva et al. 1996] for details.
-parameter, and the system is
simply the Hénon map times a rigid rotation, so that fixed points of
the Hénon map are circles of
(5). For positive A the
structure is more complicated, and as A increases, the invariant
circles can become strange attractors; see [Sosnovtseva et al. 1996] for details.
We compute stable and unstable manifolds of the quasiperiodically
forced Hénon map (5) for 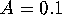 ,
, 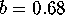 and
and 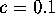 . For
these parameter values, the Hénon map has an attracting
orbit of period 2 and two saddle points. Hence,
(5) for
A = 0 has two attracting periodic circles and two circles of
saddle-type, whose stable and unstable manifolds are
two-dimensional. For
. For
these parameter values, the Hénon map has an attracting
orbit of period 2 and two saddle points. Hence,
(5) for
A = 0 has two attracting periodic circles and two circles of
saddle-type, whose stable and unstable manifolds are
two-dimensional. For 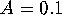 the two attracting period-two circles
and the two circles of saddle-type still exist and they are all
normally hyperbolic. One of the circles of saddle-type lies in between
the two period-two circles and the other lies far away from the
attractor. We used [Osinga 1996] to compute both circles of saddle-type
together with the linear approximation of their stable and unstable
manifolds.
the two attracting period-two circles
and the two circles of saddle-type still exist and they are all
normally hyperbolic. One of the circles of saddle-type lies in between
the two period-two circles and the other lies far away from the
attractor. We used [Osinga 1996] to compute both circles of saddle-type
together with the linear approximation of their stable and unstable
manifolds.
Our goal is to gain insight in the global dynamics. For this purpose
we compute one branch of the unstable manifold of the circle of
saddle-type that is far away from the attractor. The result is shown
in Figure 11. The computation is started at 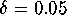 away from the circle, using 50 leaves of the foliation
away from the circle, using 50 leaves of the foliation
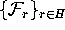 where
where 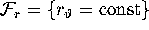 . The
intersections of the unstable manifold with the leaves
. The
intersections of the unstable manifold with the leaves 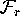 are
computed with an accuracy of
are
computed with an accuracy of 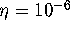 and the distance between
neighboring points on each leaf does not exceed
and the distance between
neighboring points on each leaf does not exceed 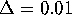 . The
colored bands on the manifold have width
. The
colored bands on the manifold have width 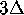 .
Figure 11 shows that the unstable manifold converges to
the attracting period-two circles by folding; the fold is clearly seen
in the enlargement of
Figure 11.
.
Figure 11 shows that the unstable manifold converges to
the attracting period-two circles by folding; the fold is clearly seen
in the enlargement of
Figure 11.
There must be
infinitely many folds, that lie extremly close to each other, because
the manifold cannot go past the other circle of saddle-type. It may be
possible to compute more folds when  is taken very small. The
computation was also performed with larger
is taken very small. The
computation was also performed with larger  . The two manifolds
were different only after the first fold; compare
Section 4.
. The two manifolds
were different only after the first fold; compare
Section 4.
We also computed the stable manifold of the other circle of saddle-type. The computations were performed with the same accuracy. One branch of this manifold must intersect the folding unstable manifold of Figure 11. Figure 12 shows that there is indeed heteroclinic tangle of the two-dimensional stable and unstable manifolds. In the animations one can see how the manifolds intersect.
We computed the stable and unstable manifolds that form the heteroclinic tangle, but we did not include the other stable and unstable manifolds in the figures. For completeness we mention that the branch of the unstable manifold in Figure 12 accumulates on the unstable manifold of the other circle. This manifold connects the two period-two attracting circles. Similarly, the branch of the stable manifold in this figure accumulates on the stable manifold of the other circle.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Wed Jul 2 10:53:36 1997