![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and ContentsThe computation of the two-dimensional stable or unstable manifold of a hyperbolic fixed point typically requires adding leaves during the computation. This is illustrated with the example
where 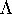 is a diagonal matrix and
is a diagonal matrix and 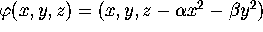 . The origin is a fixed point of f. The
eigenvalues of its linear part are the eigenvalues of
. The origin is a fixed point of f. The
eigenvalues of its linear part are the eigenvalues of 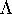 and
the corresponding eigenvectors are the coordinate axes. We take
and
the corresponding eigenvectors are the coordinate axes. We take
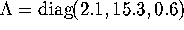 ,
,
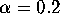 and
and 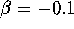 .
Due to the special form of (6), the
two-dimensional unstable manifold
.
Due to the special form of (6), the
two-dimensional unstable manifold 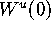 of the origin is the
of the origin is the
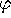 -image of the
-image of the 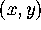 -plane. Since
-plane. Since 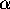 and
and 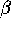 have
opposite signs, this unstable manifold is a saddle surface.
have
opposite signs, this unstable manifold is a saddle surface.
We computed 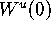 with our algorithm; see
Figure 13. The global foliation
with our algorithm; see
Figure 13. The global foliation 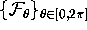 is chosen as described in
Section 3.3. The linear
approximation
is chosen as described in
Section 3.3. The linear
approximation 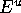 of the unstable manifold is the
of the unstable manifold is the
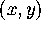 -plane. Each leaf
-plane. Each leaf 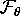 of
of 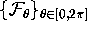 is the plane perpendicular to
is the plane perpendicular to 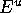 that intersects
that intersects 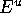 in a ray
with argument
in a ray
with argument 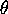 . We start the computations with a ring in
. We start the computations with a ring in 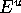 that is bounded by two circles centered at
that is bounded by two circles centered at
the origin with radii
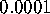 and
and 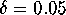 . The mesh on this first approximation is
formed by the intersection of this ring with 40 leaves of
. The mesh on this first approximation is
formed by the intersection of this ring with 40 leaves of
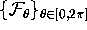 . If the distance between points on two
neighboring leaves exceeds
. If the distance between points on two
neighboring leaves exceeds 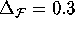 , we add an
additional leaf. We take
, we add an
additional leaf. We take 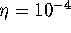 for the bisection error. The
outer circle in Figure 13 has an (arclength) radius of
for the bisection error. The
outer circle in Figure 13 has an (arclength) radius of
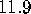 and consists of 496 mesh points. During the globalization
process, the width of the computed rings does not exceed
and consists of 496 mesh points. During the globalization
process, the width of the computed rings does not exceed
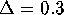 .
The colored rings in Figure 13 have width
.
The colored rings in Figure 13 have width 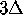 .
.
The regularity of the mesh thus obtained is shown in
Figure 14 (right), whereas
Figure 14 (left) shows the mesh for the same
manifold computed with a fixed set of 40 leaves. Because there is
an explicit formula for the global unstable manifold
of (6), we can compare it with the
numerical approximation 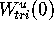 . Every point
. Every point 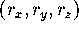 on the approximation corresponds to a point
on the approximation corresponds to a point 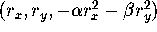 on the actual manifold, so that
the error is the difference
between the respective z-coordinates. We compute the error at the
mesh points and at the midpoints between two neighboring points on
different leaves. This error is an indication of the global error.
on the actual manifold, so that
the error is the difference
between the respective z-coordinates. We compute the error at the
mesh points and at the midpoints between two neighboring points on
different leaves. This error is an indication of the global error.
| circle radius | error fixed mesh | error adapted mesh | |||||||||
|
|
|
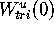 and
and
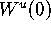 for the
saddle surface in Figure 13. The
error at circles with the given (arclength) radii is the maximum error
at the meshpoints and at the midpoints between the mesh points.
for the
saddle surface in Figure 13. The
error at circles with the given (arclength) radii is the maximum error
at the meshpoints and at the midpoints between the mesh points.
The error on circles with increasing (arclength) radius is shown in
Table 1. For the first four steps the minimum distance
of the circle to its image is smaller than 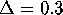 . As this
distance increases, the error increases. For distances larger than
. As this
distance increases, the error increases. For distances larger than
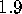 the algorithm with mesh adaptation (right column) starts adding
leaves. Because the saddle surface is
the algorithm with mesh adaptation (right column) starts adding
leaves. Because the saddle surface is 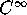 , the error in
Table 1 stays small compared to
, the error in
Table 1 stays small compared to  .
.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 21:40:51 1997