![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Because we insist that all mesh points lie in fixed
leaves, there is no accumulation of mesh points on
one-dimensional submanifolds of 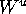 .
In this sense, our algorithm is independent of
the dynamics on the circle. For the same reason it can be used to
compute the two-dimensional unstable
manifold of a hyperbolic fixed point
.
In this sense, our algorithm is independent of
the dynamics on the circle. For the same reason it can be used to
compute the two-dimensional unstable
manifold of a hyperbolic fixed point 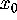 .
.
Let
Take a very small circle around
With these definitions we can use the procedure
GLOBALIZE to compute a prescribed number of
rings of
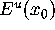 be the
two-dimensional (generalized) unstable
eigenspace of
be the
two-dimensional (generalized) unstable
eigenspace of 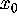 embedded in
embedded in 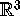 . We define the linear foliation
. We define the linear foliation
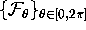 as follows.
The leaf
as follows.
The leaf 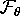 is the half-plane that
contains the ray with angle
is the half-plane that
contains the ray with angle 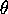 in
in
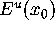 and is perpendicular to
and is perpendicular to 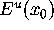 .
In fact, any linear foliation
that is transverse to
.
In fact, any linear foliation
that is transverse to 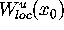 would do,
but
would do,
but  is `locally most transverse', in the sense that
each leaf is
perpendicular to
is `locally most transverse', in the sense that
each leaf is
perpendicular to 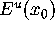 .
Let us assume that
.
Let us assume that 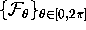 satisfies the Foliation
Condition.
satisfies the Foliation
Condition.
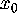 in
in
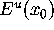 and let M be its intersection with a
prescribed finite number of leaves of
and let M be its intersection with a
prescribed finite number of leaves of
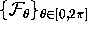 , which we take to be equally spaced in
, which we take to be equally spaced in
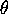 . The points in M now parametrize the
foliation, as it was the case in the previous section.
The linear approximation
. The points in M now parametrize the
foliation, as it was the case in the previous section.
The linear approximation 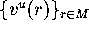 is then immediate by defining
is then immediate by defining 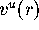 as the
unit vector in
as the
unit vector in 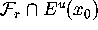 pointing
away from
pointing
away from 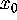 ; see Figure 8.
; see Figure 8.
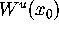 with prescribed tolerances
with prescribed tolerances
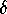 ,
,
 and
and
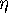 . It is clear from the
radial nature of the finite set of leaves
. It is clear from the
radial nature of the finite set of leaves
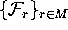 that it is necessary to
add leaves of
that it is necessary to
add leaves of 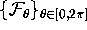 during the
computation to ensure that the maximal distance between neighboring
mesh points does not become too big.
(This effect is less pronounced for unstable manifolds
of invariant circles of saddle-type; see
Section 5.)
during the
computation to ensure that the maximal distance between neighboring
mesh points does not become too big.
(This effect is less pronounced for unstable manifolds
of invariant circles of saddle-type; see
Section 5.)
Up: 3. The algorithm
Next: 3.4
Mesh adaptation
Previous: 3.2
Globalization by adding discrete circles
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:51:59 1997