![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
It is an immediate observation that any nice,
equally spaced two-dimensional mesh
loses its nice properties under iteration of the
nonlinear map f. This has to do with different
growth rates, which lead to the accumulation of the
mesh on one-dimensional
submanifolds as is sketched in
Figure 2.
Our strategy to avoid this problem is to compute
the intersection curves
of 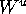 with the finitely many
leaves of
with the finitely many
leaves of 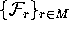 . Along each intersection curve
we impose that the mesh has a
maximal distance
. Along each intersection curve
we impose that the mesh has a
maximal distance  between meshpoints.
Furthermore, the algorithm is such that
corresponding mesh
points in neighboring leaves have the same
(arclength) distance from the invariant manifold.
This is a result of the strategy of
adding to the mesh a circle with prescribed (arclength)
distance at each step.
By default we begin with enough points in M, so
that neighboring points in M have maximal distance
between meshpoints.
Furthermore, the algorithm is such that
corresponding mesh
points in neighboring leaves have the same
(arclength) distance from the invariant manifold.
This is a result of the strategy of
adding to the mesh a circle with prescribed (arclength)
distance at each step.
By default we begin with enough points in M, so
that neighboring points in M have maximal distance
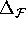 .
(It may be useful during computations to allow
the distance
.
(It may be useful during computations to allow
the distance  between mesh points in one leaf
to be different from the distance
between mesh points in one leaf
to be different from the distance 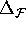 between mesh points in neighboring leaves.)
between mesh points in neighboring leaves.)
In other words, by
definition the mesh is
uniform in the beginning of the computation,
so that each edge of the triangulation
has a maximal length of
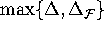 .
The only problem is that later in the computation
neighboring
points in different leaves may have a distance larger
than
.
The only problem is that later in the computation
neighboring
points in different leaves may have a distance larger
than 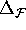 .
The solution is to
add leaves during the computation to guarantee
that the mesh stays uniform.
.
The solution is to
add leaves during the computation to guarantee
that the mesh stays uniform.
If we allow new leaves
to be added, it means that M is no longer of
fixed size. At any step, let M label the leaves
that currently define the mesh.
An additional leaf is added as follows.
After computing Mesh[k] we
check for all pairs 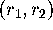 of neighboring points from M
if the distance between
of neighboring points from M
if the distance between
Mesh[k][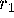
] and
Mesh[k][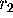
] is smaller than 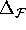 .
Suppose that this distance is larger than
.
Suppose that this distance is larger than 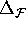 at
at 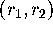 . Then we add the point
. Then we add the point
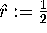
Mesh[k-1][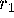
] +

Mesh[k-1][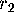
] to M,
which means that we add
the leaf 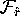 to the finite
collection defining the mesh. We
enlarge
to the finite
collection defining the mesh. We
enlarge Mesh
by the entry Mesh[k-1][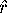
]
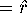 ,
that is, we enlarge the circle
,
that is, we enlarge the circle Mesh[k-1]
by the linear interpolation
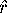 . (Note that
. (Note that
Mesh[k-1][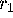
] and
Mesh[k-1][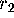
]
are less than 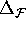 apart.)
Now we determine a new point
apart.)
Now we determine a new point
Mesh[k][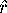
] that lies
on the curve 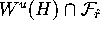 and at distance
and at distance  from
from
Mesh[k-1][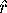
]
by the same technique we described before.
In the next step, 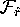 is simply
another leaf in the collection given by M, so that
the next circle will also contain a point in this
new leaf. Finally, the set of triangles in
is simply
another leaf in the collection given by M, so that
the next circle will also contain a point in this
new leaf. Finally, the set of triangles in
Tri is updated accordingly. How the mesh
grows is sketched in Figure 9;
see also Section 5.3.
![[HOME]](allfigs/logo.gif) Abstract and Contents
Abstract and Contents
Written by: Bernd Krauskopf
& Hinke Osinga
Created: May 27 1997 ---
Last modified: Fri May 30 19:52:23 1997