The Area of a Triangle
Estimating Area Some Useful Definitions Exploring Area With the Geometer's Sketchpad The Formula for the Area of Triangle Table of Contents Estimating Area Area is a measure of the space covered by a two dimensional region.
To find area: Tessalate a region with another fundamental region, then count the number of copies of the fundamental region needed to cover the original region. That count is the area.
Example: We can estimate the area of the triangles below by counting how many square units it takes to cover each triangle.
Note: When only part of a square is included in a triangle, we may be able to put it together with another part square in the triangle to form a whole square.
Area of pink = 6.
Area of blue = ____.
Area of red = ____.
Area of green = ____.
Area of yellow = ____.
Some Useful Definitions Before we start trying to find a more exact measurment of the area of a triangle, we need to define a few terms.
vertex of a triangle: the point at which two sides of a triangle meet.
altitude of a triangle: the perpendicular segment from a vertex of a triangle to the line containing the opposite side.
base of a triangle: the side of a triangle to which an altitude is drawn.
height of a triangle: the length of an altiutde.
Exploring Area With the Geometer's Sketchpad In the picture below of triangle CAT:
- line l is parallel to line k.
- point A is on line l.
- point P, point C, and point T are on line k.
- h is the height of triangle CAT.
- CT is the base of triangle CAT.
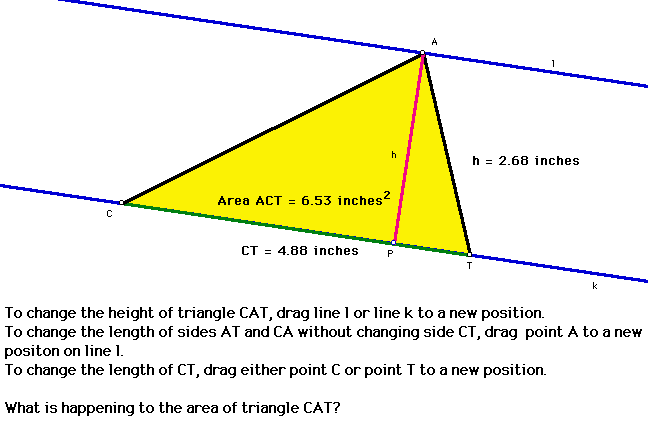
Click on the picture above to explore the area of a triangle using the Geometer's Sketchpad. Then answer the following questions using what you learned.
- Does changing the height of triangle CAT change the area of triangle CAT?
- Does changing the length of segment CA or segment AT change the area of triangle CAT?
- Does changing the base change the area of triangle CAT?
- Can you change anything else about triangle CAT? If so, what can you change and does it affect the area of triangle CAT?
- What do you think the area of a triangle depends on?
Be sure to think about these questions before going on with the lesson.
The Formula for the Area of a Triangle In the previous activity, you should have discovered that the area of a triangle depends on its height and the corresponding base.
But we still don't know how they depend on each other.
The following table contains values for the base, height, and area of certain triangles.
You can use the Geometer's Sketchpad activity from above to create different trianlges and generate additonal values to complete table.
Base of Triangle Height of Triangle Area of Triangle 2 4 4 3 4 6 1 1 1/2 2 5 5 ___ ___ ___ ___ ___ ___ ___ ___ ___ After studying the data in the table:
- What do you think the relationship between the base, height, and area of a trianlge is?
- Can you deduce a formula for finding the area of a trianlge?
- Does this formula work for the data that you have collected?
- Does your formula for other triangles?
- Does your formula work for all triangles?
Click here to check your formula.
Triangles: Everything you ever wanted to know about them